FIND SLOPE OF THE TANGENT LINE TO THE CURVE AT THE GIVEN POINT

The line which touches the curve is called tangent line.

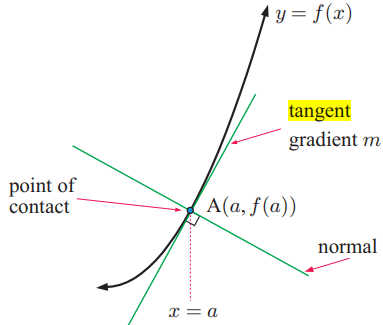
To find slope of the tangent line at the specific point, we have to follow the steps given below.

Step 1 :

Find the first derivative from the given equation of curve and derive the value of dy/dx.

Step 2 :

Apply the given point (x, y) in the slope that we have derived from the first derivative.

Step 3 :

The value of dy/dx at (x, y) is the required slope.

Use the first derivative to find the slope of the tangent line to the given curve at the given point:

Problem 1 :

y = 2x² + 6 at (-1, 8)

Solution :

y = 2x² + 6

Finding the first derivative :

dy/dx = 2(2x) + 6

dy/dx = 4x + 6

Slope at (-1, 8) 

dy/dx = 4(-1) + 6

Slope at the point (-1, 8) is 2.

Problem 2 :

y = -x² + 2x - 3 at (2, 3)

Solution :

y = -x² + 2x - 3 at (2, 3)

Finding the first derivative :

dy/dx = -2x + 2(1) + 0

dy/dx = -2x + 2

Slope at (2, 3)

dy/dx = -2(2) + 2

Slope at the point (2, 3) is 0.

Problem 3 :

y = 4 - 3x³ at (1, 1)

Solution :

y = 4 - 3x³ at (1, 1)

Finding the first derivative :

dy/dx = 4 - 3(3x²)

dy/dx = 4 - 9x²

Slope at (1, 1)

dy/dx = 4 - 9(1)²

= -5

Slope at the point (1, 1) is -5.

Problem 4 :

Solution :

Problem 5 :

Tangent lines are drawn to the parabola

y = x² at (2, 4) and (-1/8, 1/64)

Prove the tangents are perpendicular.

Solution :

y = x²

By proving the slopes of the tangent drawn at the specific points given, we can prove the tangent lines are perpendicular.

Finding the first derivative :

dy/dx = 2x

Slope at (2, 4) :

dy/dx = 2(2) ==> 4 ----(1)

Slope at (-1/8, 1/64) :

dy/dx = 2(-1/8) ==> -1/4 ----(2)

(1) x (2)

= 4 (-1/4)

Product of the slopes = -1

So, the tangents drawn at the points (2, 4) and (-1/8, 1/64) for the parabola, they are perpendicular.

Problem 6 :

Find a point on the parabola

y = -x² +3x + 4

where the slope of the tangent line is 5.

Solution :

y = -x² +3x + 4

dy/dx = -2x + 3(1) + 0

dy/dx = -2x + 3

Slope of the tangent line = 5

-2x + 3 = 5

-2x = 5 - 3

-2x = 2

x = -1

When x = -1, y = -x² +3x + 4

y = -(-1)² +3(-1) + 4

y = -1-3+4

y = 0

So, the required point is (-1, 0).

Problem 7 :

Find the slope of the tangent line to the graph of

3x² + 5 lny = 12 at (2, 1) is 

A)  -12/5      B)  12/5        C)  5/12       D)  12      E)  -7

Solution :

3x² + 5 lny = 12

Finding the first derivative :

3(2x) + 5(1/y) (dy/dx) = 0

6x + (5/y)(dy/dx) = 0

dy/dx = -6x(y/5)

dy/dx = -6xy/5

Applying the point (2, 1)

dy/dx = -6(2)(1)/5

= -12/5

So, the required slope is -12/5. Option A.

Problem 8 :

Solution :

So, the required value of y is 58/7, option C.