FIND THE RADIUS AND DIAMETER OF EACH CIRCLE

Problem 1 :

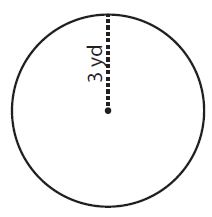
Solution :

By observing the figure,

Radius (r) = 3 yd

To find the diameter of a circle, (d) = 2 × r

= 2 × 3

Diameter (d) = 6 yd

Problem 2 :

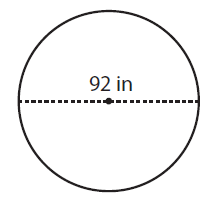
Solution :

By observing the figure,

Diameter (d) = 92 in

To find the radius of a circle, (r) = D/2 

= (92)/2

Radius (r) = 46 in

Problem 3 :

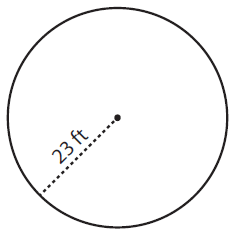
Solution :

By observing the figure,

Radius (r) = 23 ft

To find the diameter of a circle, (d) = 2 × r

= 2 × 23

Diameter (d) = 46 ft

Problem 4 :

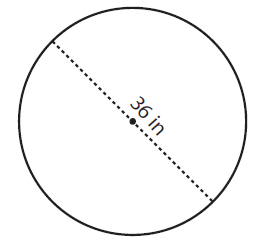
Solution :

By observing the figure,

Diameter (d) = 36 in

To find the radius of a circle, (r) = D/2 

= 36 in/2

Radius (r) = 18 in

Problem 5 :

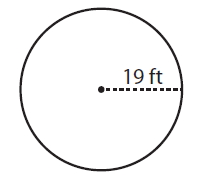
Solution :

By observing the figure,

Radius (r) = 19 ft

To find the diameter of a circle, (d) = 2 × r

= 2 × 19 ft

Diameter (d) = 38 ft

Problem 6 :

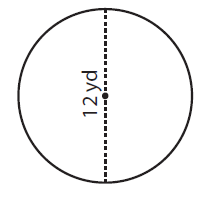
Solution :

By observing the figure,

Diameter (d) = 12 yd

To find the radius of a circle, (r) = D/2 

= 12 yd/2

Radius (r) = 6 yd

Problem 7 :

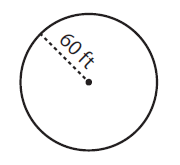
Solution :

By observing the figure,

Radius (r) = 60 ft

To find the diameter of a circle, (d) = 2 × r

= 2 × 60 ft

Diameter (d) = 120 ft

Problem 8 :

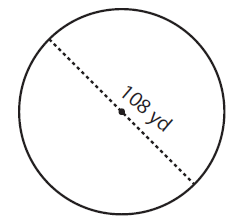
Solution :

By observing the figure,

Diameter (d) = 108 yd

To find the radius of a circle, (r) = D/2 

= 108 yd/2

Radius (r) = 54 yd

Problem 9 :

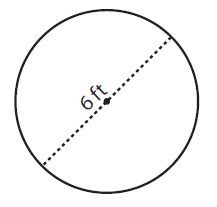
Solution :

By observing the figure,

Diameter (d) = 6 ft

To find the radius of a circle, (r) = D/2 

= 6 ft/2

Radius (r) = 3 ft

Problem 10 :

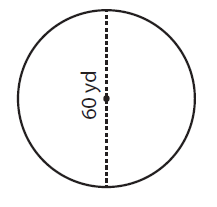
Solution :

By observing the figure,

Diameter (d) = 60 yd

To find the radius of a circle, (r) = D/2 

= 60 yd/2

Radius (r) = 30 yd

Problem 11 :

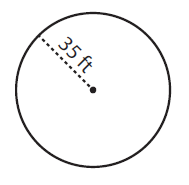
Solution :

By observing the figure,

Radius (r) = 35 ft

To find the diameter of a circle, (d) = 2 × r

= 2 × 35 ft

Diameter (d) = 70 ft

Problem 12 :

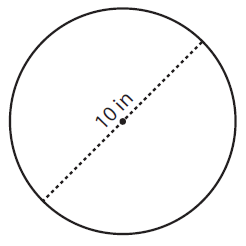
Solution :

By observing the figure,

Diameter (d) = 10 in

To find the radius of a circle, (r) = D/2 

= 10 in/2

Radius (r) = 5 in

Problem 13 :

The cirucmference of the roll of cautiontape decreases 10.5 inches after a construction worker uses some of the tape. Which is the best estimate of the diameter of the roll after the decrease ?

a)  5 inches    b)  7 inches     c)  10 inches      d)  12 inches

Solution :

After the decrease, the circumference of the roll is

31.4 − 10.5 = 20.9 inches.

C = π d

20.9 ≈ 3.14 ⋅ d

21 ≈ 3d 

Divide each side by 3

d = 21/3

d = 7

So, option b is correct.

Problem 14 :

A semicircle is one-half of a circle. Find the perimeter of the semicircular region

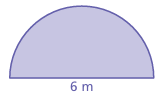
Solution :

The straight side is 6 meters long. The distance around the curved part is one-half the circumference of a circle with a diameter of 6 meters.

C/2 = π d / 2 

≈ (3.14 ⋅ 6) / 2

= 9.42

So, the perimeter is about 6 + 9.42 = 15.42 meters.

Problem 15 :

A circular sinkhole has a circumference of 75.36 meters. A week later, it has a circumference of 150.42 meters.

a. Estimate the diameter of the sinkhole each week.

b. How many times greater is the diameter of the sinkhole now compared to the previous week?

Solution :

a)  Let d and D be the diameters of small circular sinkhole and large circular sinkhole.

π d = 75.36 

π D = 150.42

Applying π = 3.14, we get

d = 75.36/3.14 and D = 150.42/3.14

d = 24 and D = 47.9 (approximately) 48 meter

Diameter of the sinkhole for the first week is 24 meter and diameter of the sinkhole after one week is 48 meters.

b)  Number of times greater = 48/24

= 2 times

Problem 16 :

Consider the circles A, B, C, and D.

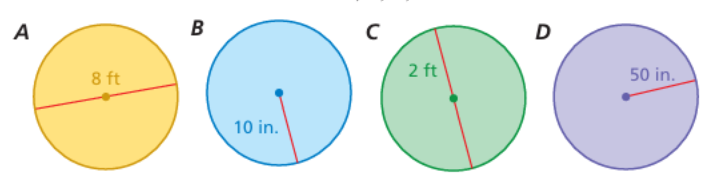
a. Without calculating, which circle has the greatest circumference?

b. Without calculating, which circle has the least circumference?

Solution :

To have a conclusion that which circle has greater circumference, let us find the radius of each circle.

Circle A :

Given that, diameter of circle A = 8 ft

radius = 4 ft

1 ft = 12 inches

4 ft = 48 inches

Circle B :

radius of circle B = 10 inches

Circle C :

diameter of circle C = 2 ft

radius = 1 ft

1 ft = 12 inches

Circle D :

Radius of circle D = 50 inches

Comparing all radii, circle D has larger radius, then this circle will have greater circumference.

b)  Circle C has least circumference, because it has lesser radius.