FIND THE MISSING SIDE OF THE TRIANGLE INSCRIBED IN A SEMICIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The angle created in a semicircle is 90°. Then, we will be having a right triangle. Using Pythagorean theorem, we can find the missing side of a right triangle.
Calculate
the length of sides labelled in the circles below
Problem 1 :
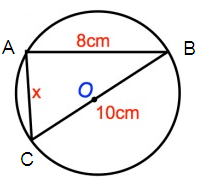
Solution :
Here ∠BAC = 90
Using Pythagorean theorem :
AB2 + AC2 = BC2
82 + x2 = 102
64 + x2 = 100
x2 = 100 – 64
x2 = 36
x = 6
So, the value of x is 6 cm.
Problem 2 :
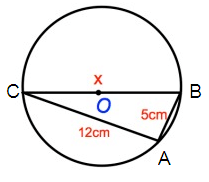
Solution :
∠BAC = 90
Using Pythagorean theorem :
AB2 + AC2 = BC2
52 + 122 = x2
25 + 144 = x2
x2 = 144 + 25
x2 = 169
x = 13
So, the value of x is 13 cm.
Problem 3 :
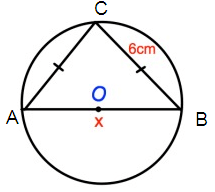
Solution :
AC2 + BC2 = AB2
62 + 62 = x2
36 + 36 = x2
72 = x2
x = 8.48
So, the value of x is 8.48 cm.
Calculate
the length of sides labelled in the circles below
Problem 4 :
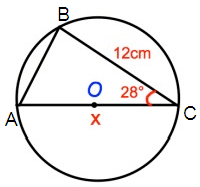
Solution :
In the right triangle ABC,
AB = Opposite side, AC = Adjacent side and BC = Hypotenuse
cos θ = Adjacent side / Hypotenuse
cos 28 = AC/BC
cos 28º = x/12
0.882 = x/12
x = 0.882(12)
x = 10.58
So, the value of x is 10.58.
Problem 5 :
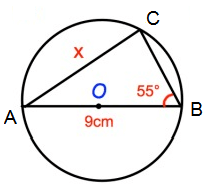
Solution :
In the right triangle ABC,
AB = Hypotenuse, AC = Opposite side and BC = Adjacent side.
sin 55º = opposite/hypotenuse
= AC/AB
= x/9
0.82 = x/9
x = 0.82 × 9
x = 7.38
So, the value x is 7.38.
Problem 6 :
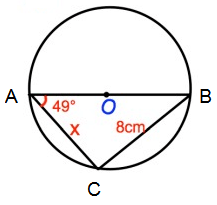
Solution :
In the right triangle ABC, AB = Hypotenuse, BC = Opposite side and AC = Adjacent side
tan 49º = opposite/adjacent
tan 49 = BC/AC
1.15 = 8/AC
AC = 8/1.15
AC = 6.95
AC = 7 cm
So, the value of x is 7 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling