FIND THE MISSING SIDE OF RECTANGLE WHEN AREA IS GIVEN

To find area of rectangle, we use the formula 

Area = length x width

By applying the known values, we can solve for unknown.

Problem 1 :

Mr. Fitch hires a landscape architect to renovate his front yard. The rectangular yard is 30 feet long. If the area of the yard is 600 square feet, determine the width of the yard.

Solution :

Area of front yard = 600 square feet

Length = 30 feet

Area of rectangle = length × width

600 = 30 × width

Width = 600/30

Width = 20 feet

So, width of the front yard is 20 feet.

Problem 2 :

The screen of an LED TV measures 32 inches in length and its area is 896 square inches. What is the width of the screen?

Solution :

Area of the screen = 896 square inches

Length = 32 inches

Area of rectangle = length × width

896 = 32 × width

Width = 896/32

Width = 28 inches

So, width of the screen is 28 inches.

Problem 3 :

The area of an apple orchard is 4,675 square feet. Find the length of the rectangular orchard, if its width is 55 feet.

Solution :

Area of the orchard = 4,675 square feet

Width = 55 feet

Area of rectangle = length × width

4675 = length × 55

Length = 4675/55

Length = 85 feet

So, length of the orchard is 85 feet.

Problem 4 :

The area of an aluminum sheet is 124.32 square feet. If its length is 22.2 feet, what is the width of the aluminum sheet?

Solution :

Area of the aluminum sheet = 124.32 square feet

Length = 22.2 feet

Area of rectangle = length × width

124.32 = 22.2 × width

Width = 124.32 / 22.2

Width = 5.6 feet

So, width of the aluminum sheet is 5.6 feet.

Problem 5 :

Ted’s rectangular corn field has an area of 2,280 square feet. What is the length of the field, if its width measures 28.5 feet?

Solution :

Area of the rectangular corn field = 2,280 square feet

Width = 28.5 feet

Area of rectangle = length × width

2280 = length × 28.5

Length = 2280/28.5

Length = 80 feet

So, length of the field is 80 feet.

Problem 6 :

The green chalkboard in the kindergarten classroom is 24 inches wide. If the area of the board is 864 square inches, find the length of the board.

Solution :

Area of the board = 864 square inches

Width = 24 inches

Area of rectangle = length × width

864 = length × 24

Length = 864/24

Length = 36 inches

So, length of the board is 36 inches.

Problem 7 :

A playground in Bucks Country has an area of 300 square yards. If the width of the rectangular playground is 15 yards, find the length of the playground.

Solution :

 Area of the playground = 300 square yards

Width = 15 yards

Area of rectangle = length × width

300 = length × 15

Length = 300/15

Length = 20 yards

So, length of the playground is 20 yards.

Problem 8 :

A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?

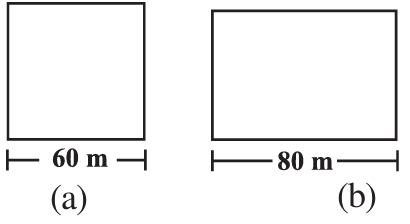
Solution :

Perimeter of square = 4(side length)

Side length of square = 60 cm

= 4(60)

= 240 cm

Perimeter of rectangle = 2(length + width)

Length of rectangle = 80 m, width of the rectangle = w

240 = 2(80 + w)

Solving for w, we get

240/2 = 80 + w

120 = 80 + w

w = 120 - 80

w = 40 cm

So, width of the rectangle is 40 cm.

Problem 9 :

The diagonal of a rectangle is √41 cm and its area is 20 square cm. The perimeter of the rectangle must be 

a)  9 cm   b)  18 cm   c)  20 cm     d)  41 cm

Solution :

Area of rectangle = 20 square cm

Diagonal of rectangle = √41

let l be the length and w be the width.

lw = 20

w = 20/l

l² + w² = (√41)²

l² + w² = 41

l² + (20/l)² = 41

l² + (400/l²) = 41

l⁴ + 400 = 41l²

l⁴ - 41l² + 400 = 0

Let t = l²

t² - 41t + 400 = 0

(t - 25)(t - 16) = 0

t = 25 and t = 16

 l² = 25 and  l² = 16 

l = 5 and l = 4

When l = 5, w = 20/5 ==> 4

When l = 4, w = 20/4 ==> 5

Perimeter of rectangle = 2(5 + 4) 

= 2(9)

= 18 cm

So, option b is correct.

Problem 10 :

A rectangular carpet has an area of 60 sq.m. If its diagonal and longer side together equal 5 times the shorter side, the length of the carper is

a) 5 m   b)  12 m    c)  13 m   d)  14.5 m

Solution :

Area of rectangle = 60 sq.m

Let x be the shorter side.

Diagonal = 5x

(5x)² = x² + length²

25x² - x² = length²

length² = 24 x²

length = √24 x²

= 2x√3

x(2x√3) = 60

x²(2√3) = 60

x² = 60/2√3

x² = 60/3.464

= 17.32

x = √17.32

x = 4.16 cm

Length = 2(4.16)(1.732)

= 14.41

Approximately 14.5 m, option d is correct.