FIND THE MISSING SIDE OF A RIGHT TRIANGLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The square of hypotenuse is equal to sum of squares of other two sides.
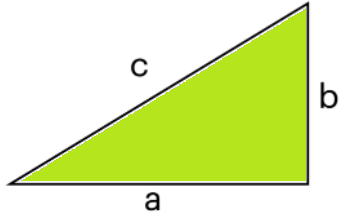
c2 = a2 + b2
Find the values of the unknowns in the following triangles :
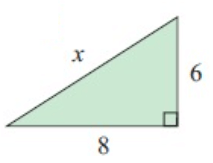
Problem 1 :
Solution :
Using
Pythagorean theorem.
x2 = 62 + 82
x2 = 36 + 64
x2 = 100
x = 10
So, the unknown value is 10.
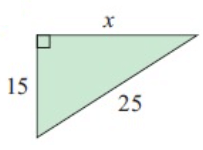
Problem 2 :
Solution :
(25)2 = (15)2 + x2
625 = 225 + x2
625 – 225 = x2
400 = x2
20 = x
So, the unknown value is 20.
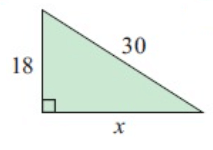
Problem 3 :
Solution :
(30)2 = (18)2 + x2
900 = 324 + x2
900 – 324 = x2
576 = x2
24 = x
So, the unknown value is 24.
Problem 4 :

Solution :
x2 = 22 + (1.5)2
x2 = 4 + 2.25
x2 = 6.25
x = 2.5
So, the unknown value is 2.5.
Problem 5 :
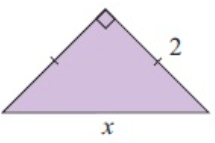
Solution :
x2 = 22 + 22
x2 = 4 + 4
x2 = 8
x = 2.828
So, the unknown value is 2.828.
Problem 6 :

Solution :
x2 = 32 + 32
x2 = 9 + 9
x2 = 81
x = 9
So, the unknown value is 9`.
Problem 7 :
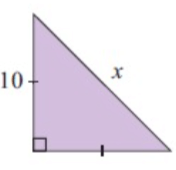
Solution :
By observing the figure.
Using Pythagorean theorem.
x2 = (10)2 + (10)2
x2 = 100 + 100
x2 = 200
x = 14.14
So, the unknown value is 14.14.
Problem 8 :
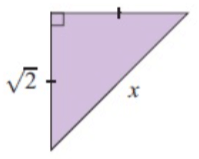
Solution :
x2 = (√2)2 + (√2)2
x2 = 2 + 2
x2 = 4
x = 2
So, the unknown value is 2.
Problem 9 :
Find the value of x. Then tell whether the side lengths form a Pythagorean triple.
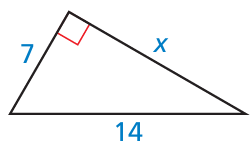
Solution :
Using Pythagorean theorem,
142 = 72 + x2
196 = 49 + x2
x2 = 196 - 49
x2 = 147
x = √147
x = √(3 x 7 x 7)
x = 7 √3
Problem 10 :
The skyscrapers shown are connected by a skywalk with support beams. Use the Pythagorean Theorem to approximate the length of each support beam
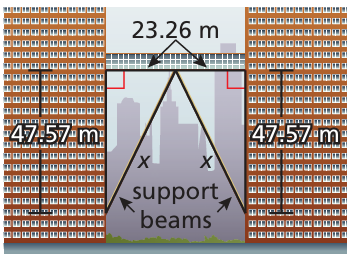
Solution :
x2 = 23.262 + 47.572
x2 = 541.02 + 2262.90
= 2803.92
x = √2803.92
x = 52.95
x = 53 m approximately
Problem 11 :
An anemometer is a device used to measure wind speed. The anemometer shown is attached to the top of a pole. Support wires are attached to the pole 5 feet above the ground. Each support wire is 6 feet long. How far from the base of the pole is each wire attached to the ground?
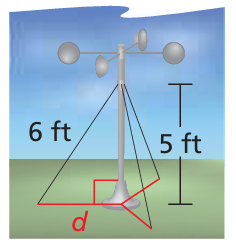
Solution :
62 = d2 + 52
36 = d2 + 25
d2 = 36 - 25
d2 = 11
d = √11
= 3.31 ft
So, the required distance is 3.31 ft
Problem 12 :
Determine the area of the indicated square in each of the following diagrams.
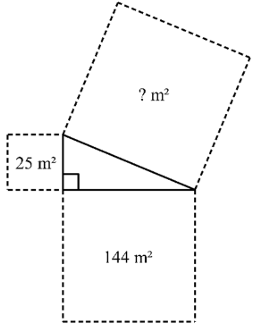
Solution :
Area of square at the left = 25 m2
Side length of square at left = √25
= 5 m
Area of square at the bottom = 144 m2
Side length of square at the bottom = √144
= 12 m
Let x be the side length of square at the top.
Inside the triangle, using Pythagorean theorem
x2 = 52 + 122
x2 = 25 + 144
x2 = 169
x = √169
x = 13 m
Area of square at the top is 169 m2
Problem 13 :
For each of the following, use the given areas to determine side lengths a, b and c.
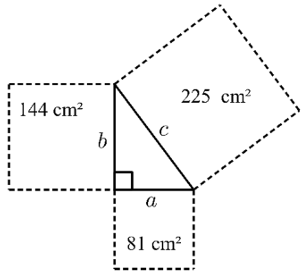
Solution :
Area of square at the left = 144 cm2
Side length of square at left = √144
b = 12 cm
Area of square at the bottom = 81 cm2
Side length of square at the bottom = √81
a = 9 cm
Area of square at the top = 225 cm2
Side length of square at the top = √225
c = 15 cm
Problem 14 :
You are making a kite and need to figure out how much binding to buy. You need the binding for the perimeter of the kite. The binding comes in packages of two yards. How many packages should you buy
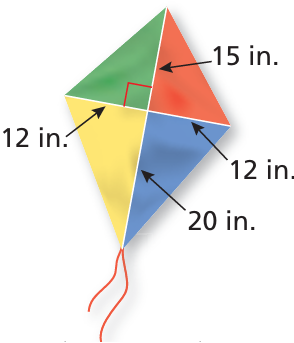
Solution :
Let x be the the length of hypotenuse of green triangle
x2 = 122 + 152
x2 = 144 + 225
x2 = 369
x = √369
x = 19.2 inches
Let x be the the length of hypotenuse of yellow triangle
x2 = 122 + 202
x2 = 144 + 400
x2 = 544
x = √544
x = 23.3 inches
Perimeter of kite = 2(19.2) + 2(23.3)
= 2(19.2 + 23.3)
= 2(42.5)
= 85 inches
1 yard = 36 inches
1 inch = 1/36 yard
85 inches = 85/36
= 2.4 yards
More than 1 package is needed.
Problem 15 :
Describe and correct the error in using the Pythagorean Theorem
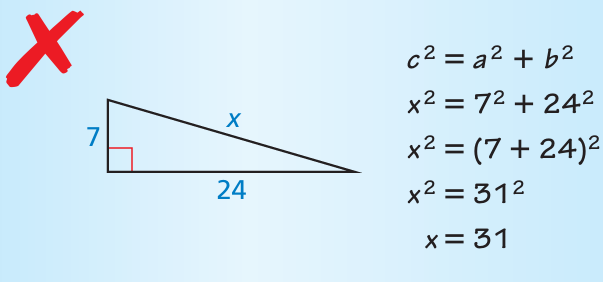
Solution :
Using Pythagorean theorem, finding the missing side.
x2 = 72 + 242
x2 = 49 + 576
x2 = 625
x = √625
x = 25
This is the error.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling