FIND THE MISSING SIDE IN SIMILAR FIGURES

Find x given that the figures are similar :

Problem 1 :

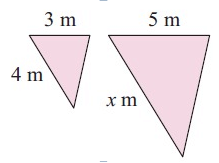
Solution :

By observing the figure,

If two shapes are similar, then corresponding sides will be in the same ratio.

4/x = 3/5

Using cross multiplication, we get

3x = 20

Dividing both sides by 3.

3x/3 = 20/3

x = 6 2/3 m

Problem 2 :

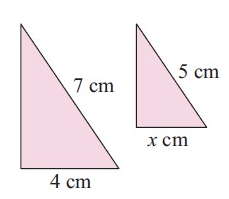
Solution :

Comparing the corresponding sides, we get

4/x = 7/5

Using cross multiplication, we get

7x = 20

Dividing both sides by 7.

7x/7 = 20/7

x = 2 6/7 cm

Problem 3 :

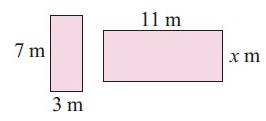
Solution :

Comparing the corresponding sides, we get

7/11 = 3/x

Using cross multiplication, we get

7x = 33

Dividing both sides by 7.

7x/7 = 33/7

x = 4 5/7 m

Problem 4 :

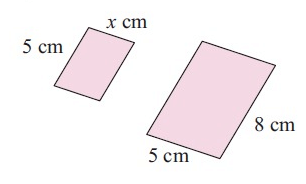
Solution :

Comparing the corresponding sides, we get

5/8 = x/5

Using cross multiplication, we get

8x = 25

Dividing both sides by 8.

8x/8 = 25/8

x = 3 1/8 cm

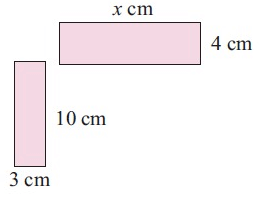
Problem 5 :

Solution :

Comparing the corresponding sides, we get

3/4 = 10/x

Using cross multiplication, we get

3x = 40

Dividing both sides by 3.

3x/3 = 40/3

x = 13 1/3 cm

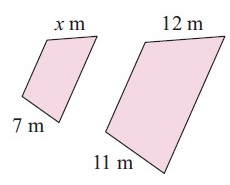
Problem 6 :

Solution :

Comparing the corresponding sides, we get

7/11 = x/12

Using cross multiplication, we get

11x = 84

Dividing both sides by 11.

11x/11 = 84/11

11x = 84

x = 84/11 m

Problem 7 :

A town plans to build a new swimming pool. An Olympic pool is rectangular with a length of 50 meters and a width of 25 meters. The new pool will be similar in shape to an Olympic pool but will have a length of 40 meters. Find the perimeters of an Olympic pool and the new pool

Solution :

Length of Olympic pool = 50 meters

Width of Olympic pool = 25 meters

Length of pool similar to the olympic pool = 40 meters

Let x be the width of the similar pool

50 : 25 = 40 : x

50/25 = 40/x

2 = 40/x

x = 40/2

x = 20

So, the required width of the pool similar to Olympic pool is 20 meters.

Problem 8 :

In the diagram, △ABC ∼ △DEF. Find the area of △DEF.

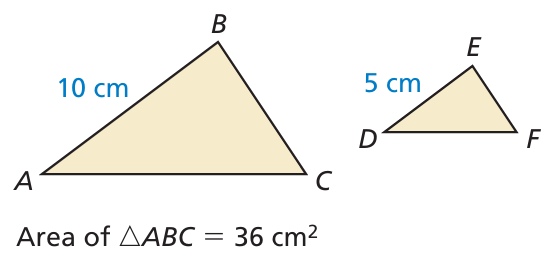
Solution :

When two shapes are similar, the square of the ratio between the similar sides will be equal to the ratio of their area.

(AB/DE)² = Area of triangle ABC/Area of triangle DEF

(10/5)² = 36/Area of triangle DEF

2² = 36/Area of triangle DEF

4 = 36/Area of triangle DEF

Area of triangle DEF = 36/4

= 9 cm²

So, the area of the triangle DEF is 9 cm²

Problem 9 :

A school gymnasium is being remodeled. The basketball court will be similar to an NCAA basketball court, which has a length of 94 feet and a width of 50 feet. The school plans to make the width of the new court 45 feet. Find the perimeters of an NCAA court and of the new court in the school.

Solution :

Measures of NCAA basketball court :

Length = 94 feet and width = 50 feet

Perimeter of NCAA = 2(length + width)

= 2(94 + 50)

= 2(144)

= 288 feet

Measures of similar plan :

Let x be the length of basket ball court.

Width of the school basket ball court = 45 feet

ratio of similar sides = ratio of the perimeters of the shapes

50/45 = 288/Perimeter of new court similar to NCAA

1.11 = 288/Perimeter of new court similar to NCAA

Perimeter of new court similar to NCAA = 288/1.11

= 259 feet 

Problem 10 :

Describe and correct the error in finding the area of rectangle B. The rectangles are similar.

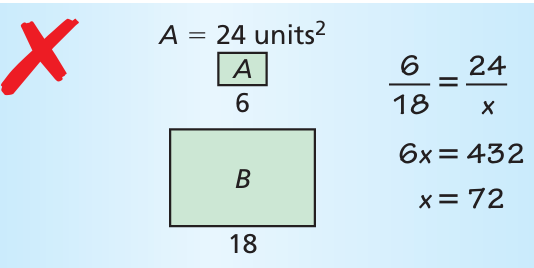
Solution :

When two shapes are similar, the square of the ratio between the similar sides will be equal to the ratio of their area.

(6/18)² = (24/x)

(1/3)² = (24/x)

1/9 = 24/x

x = 24(9)

= 216

So, the area of the large rectangle is 216 square units.

Problem 11 :

In the following the two polygons are similar. Find the values of x and y.

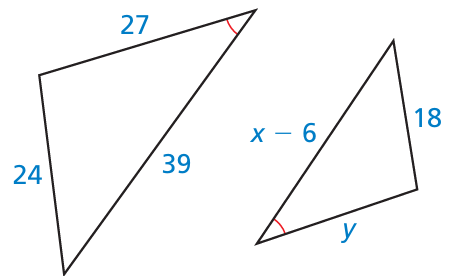
Solution :

Since the shapes are similar,

Problem 12 :

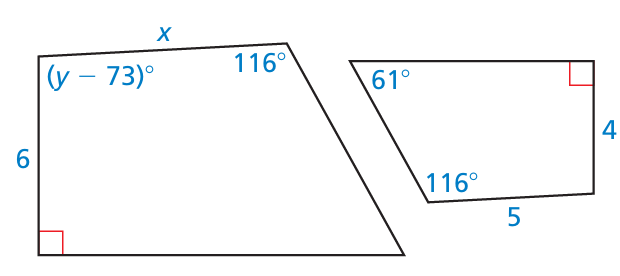
Solution :

6/4 = x/5

6(5) = 4x

x = 30/4

x = 7.5

Sum of interior angles of the quadrilateral = 360

Let x be the missing angle

61 + 116 + 90 + x = 360

267 + x = 360

x = 360 - 267

x = 93

93 = y - 73

y = 93 + 73

y = 166

Problem 13 :

In table tennis, the table is a rectangle 9 feet long and 5 feet wide. A tennis court is a rectangle 78 feet long and 36 feet wide. Are the two surfaces similar? Explain. If so, find the scale factor of the tennis court to the table.

Solution :

9/78 = 5/36

0.11 ≠ 0.13

The surface is not similar.