FIND THE MISSING MEASUREMENTS OF PARALLELOGRAM

In the following parallelogram AB is base and the line drawn from D to AB is height.

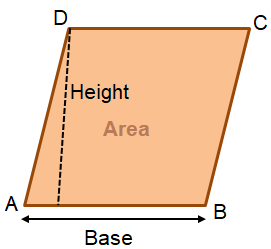
Area of parallelogram = Base x height

Problem 1 :

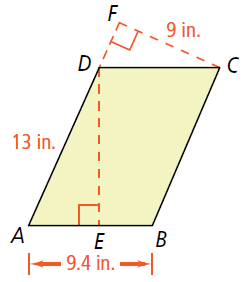
For the parallelogram ABCD, what is DE to the nearest tenth?

Solution :

Area of parallelogram =  Base x height

Base (AB) = 9.4 in and height (DE) = ?

Base (AD) = 13 in and height (CF) = 9 in

9.4 x DE = 13 x 9

DE = (13 x 9)/9.4

DE = 12.4 in

Problem 2 :

Solution :

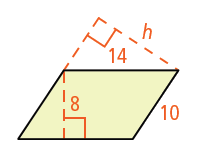
Area of the parallelogram = base x height

When base = 14, height = 5

When base = 10, height = ?

Let h be the required height.

14 x 5 = 10 x h

h = (14 x 5)/10

h = 7

So, the required height is 7.

Problem 3 :

Solution :

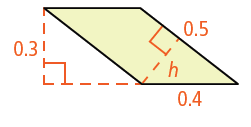
When base = 0.4, height = 0.3

When base = 0.5 and height =  h

0.4 x 0.3 = 0.5 x h

h = (0.4 x 0.3)/0.5

h = 0.24

So, the required height is 0.24.

Problem 4 :

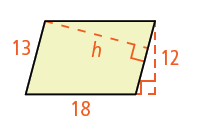
Solution :

When base = 13, height = h

When base = 18, height = 12

13 x h = 18 x 12

h = (18 x 12)/13

h = 16.61

So, the required height is 16.61.

Problem 5 :

The area of a parallelogram is 24 in², and the height is 6 in. Find the length of the corresponding base.

Solution :

Area of parallelogram = 24 in²

height = 6 in

Let base = b

b x 6 = 24

b = 24/6

b = 4 in

So, the required base is 4 inches.

Problem 6 :

Find the area of the composite figure. Then find the area.

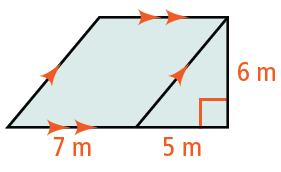
Solution :

The shape given above includes two basic shapes, parallelogram and right triangle.

Area of the shape = Area of parallelogram + area of triangle

Base of the parallelogram = 7 m and height = 6 m

Base of right triangle = 5 m and height = 6 m

 = 7 x 6 + (1/2) x 5 x 6

 = 42 + 15

 = 57 m²