FIND THE MISSING DIMENSION OF A TRAPEZOID

A trapezoid is also known as a trapezium is a four-sided polygon or a quadrilateral. It has one set of opposite sides which are parallel and a set of non-parallel sides.

The parallel sides are known as the bases and the non-parallel sides are known as the legs of the trapezoid.

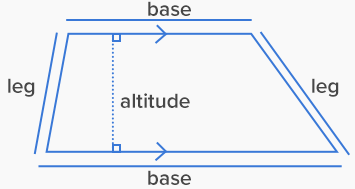
Area of trapezoid = (1/2) h (a + b)

Here a and b area parallel sides and h is height.

Perimeter of the trapezoid = Sum of length of all sides.

Find x.

Problem 1 :

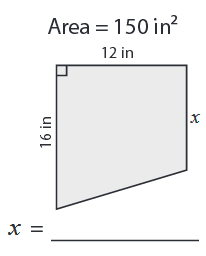
Solution :

So, the value of x is 6.

Problem 2 : 

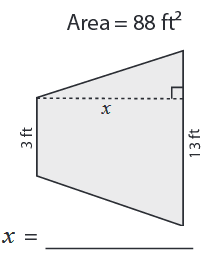
Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 88 ft², a = 3 ft, b = 13 ft and h = x

88 = (1/2) ⋅ h (3 + 13)

Multiply by 2 on both sides

88 ⋅ 2 = x (16)

Divide by 16 on both sides.

(88 ⋅ 2)/16 = h

h = 11

Problem 3 :

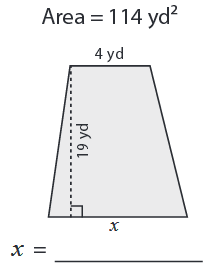
Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 114 yd², a = 4 yd, b = x and h = 19 yd

114 = (1/2) ⋅ 19 (4 + x)

(114 ⋅ 2) = 19 (4 + x)

Divide by 19 on both sides.

(114 ⋅ 2)/19 = 4 + x

4 + x = 12

Subtracting 4 on both sides.

x = 8

So, base length of the trapezoid is 8 yd.

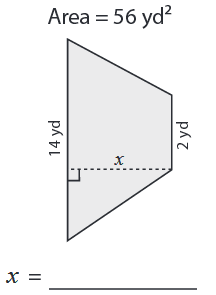
Problem 4 :

Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 56 yd², a = 14 yd, b = 2 yd and h = x

56 = (1/2) ⋅ x (14 + 2)

(56 ⋅ 2) = x (16)

Divide by 16 on both sides.

(56 ⋅ 2)/16 = x

x = 7 yd

So, height of the trapezoid is 7 yd.

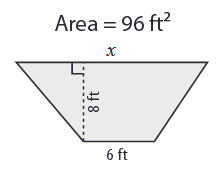
Problem 5 :

Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 96 ft², a = 6 ft, b = x and h = 8 ft

96 = (1/2) ⋅ 8 (6 + x)

96 = 4 (6 + x)

Divide by 4 on both sides.

96/4 = 6 + x

6 + x = 24

Subtracting 6 on both sides.

x = 24 - 6

x = 18 ft

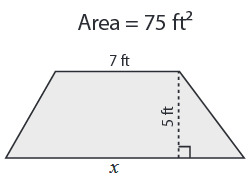
Problem 6 :

Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 75 ft², a = 7 ft, b = x and h = 5 ft

75 = (1/2) ⋅ 5 (7 + x)

Divide by 4 on both sides.

75/5 = (1/2) (7 + x)

(1/2) (7 + x) = 15

6 + x = 24

Subtracting 6 on both sides.

x = 24 - 6

x = 18 ft

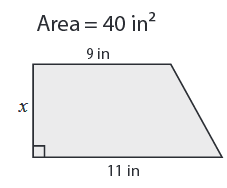
Problem 7 :

Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 40 in², a = 9 in, b = 11 in and h = x in

40 = (1/2) ⋅ x (9 + 11)

Multiply by 2 on both sides.

(40⋅2) = x(20)

Divide by 20 on both sides.

x = 2⋅2

x = 4 in

Problem 8 :

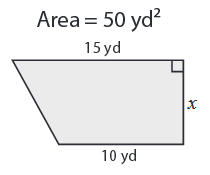
Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 50 yd², a = 15 in, b = 10 yd and h = x yd

50 = (1/2) ⋅ x (15 + 10)

Multiply by 2 on both sides.

(50⋅2) = x(25)

Divide by 25 on both sides.

x = 100/25

x = 4 yd

Problem 9 :

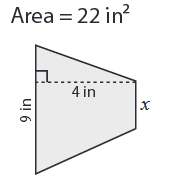
Solution :

Area of trapezoid A = (1/2) h (a + b)

Area = 22 in², a = 9 in, b = x and h = 4 in

22 = (1/2) ⋅ 4 (9 + x)

Multiply by 2 on both sides.

(22⋅2) = 4(9+x)

Divide by 4 on both sides.

9 + x = 44/4

x = 11 - 9

x = 2 in

x = 4 yd

Problem 10 :

You can use a trapezoid to approximate the shape of Scott County, Virginia. The population is about 23,200. About how many people are there per square mile?

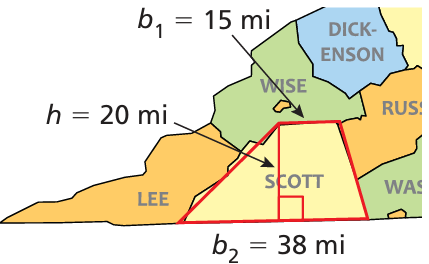
Solution :

b₁ = 15 miles and b₂ = 38 miles and height = 20 miles

The population = 23200

Area = (1/2) ⋅ 20 (15 + 38)

= 10 (53)

= 530 square miles

The area of Scott County is about 530 square miles. Divide the population by the area to fi nd the number of people per square mile.

Number of people in per square mile = 23200/530

= 43.77

Approximately 44 people.

Problem 11 :

What is the area of the shaded figure shown below?

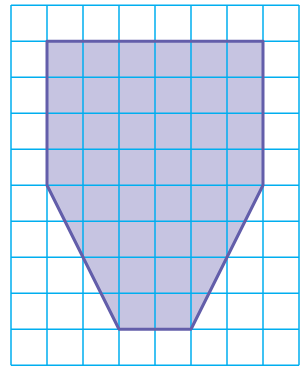
a) 32 units²         b) 40 units²       c) 44 units²      d) 56 units²

Solution :

Area of the shape = Area of trapezoid + area of rectangle

= (1/2) x h(a + b) + length x width

= (1/2) x 4(6 + 2) + 6 x 4

= 2(8) + 24

= 16 + 24

= 40 units²

So, option b is correct.