FIND THE LEAST NUMBER WHEN DIVIDED BY TO MAKE PERFECT SQUARE

Problem 1 :

Find the least number by which 384 must be divided to make it a perfect square 

Solution :

384 is not a perfect square. Accordingly the given information, we have to divide 384 should be divided by some integer inorder to make it as perfect square.

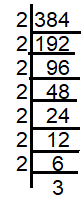
Grouping the terms as pairs 

2 x 2 x 2 x 2 x 2 x 2 x 2 x 3

Here 2 x 3 is like extra, if we remove 6 it will become a perfect square.

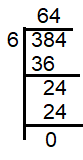
Dividing 384 by 6, we get the quotient as 64 which is perfect square.

Problem 2 :

The least number by which 125 must be divided to make it a perfect square is

Solution :

125 is not a perfect square, to find by which number it should be divided to make it as perfect square, let us write 125 as product of prime factors.

125 = 5 x 5 x 5

Grouping as pairs, we get one extra 5. 

So, 125 should be divided by 5 to make it as perfect square.

Problem 3 :

By which least number should 1176 be divided to make it a perfect square? find the perfect square number. also find the square root

Solution :

To find the least number that should be divided 

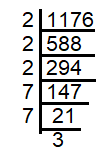
1176 = 2 x 2 x 2 x 7 x 7 x 3

Here 2 and 3 are extra, by dividing 1176 by 6 we can get a number which is perfect square.

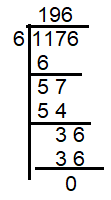
By dividing 1176 by 6, we get quotient as 196 which is perfect square.

√196 = √14 x 14

= 14

Square root of perfect square number is 14.

Problem 4 :

The area of a square field is 1476225 sqm. A motorist travels along its boundary at 36 km/hr. In how much time, will he return to the start point ?

Solution :

 Area of square field = 1476225

√1476225 = √(5² x 3¹⁰)

= 5 x 3⁵

= 1215 m

Converting km/h to m/sec

36 km/hr = 36 x (5/18) m/sec

= 10 m/sec

One side length = 1215

Side length or length of the boundary line = 4(1215)

Speed = 10 m/sec

Time = distance / speed

= 4(1215) / 10

= 486 seconds

Converting into hours, we get

= 486/60

= 8.1 hours

8 hours and 10 minutes.

Problem 5 :

The least number by which 72 be divided to make it a perfect square is _____________.

Solution :

Expressing 72 as product of prime numbers, we get

72 = 2 x 2 x 2 x 3 x 3

Grouping them as pairs, we find one 2 as extra. By removing it,

= 2 x 2 x 3 x 3

= 36 (is a perfect square)

So, 72 should be divided by the least number 2 to convert it as perfect square.

Problem 6 :

By what smallest number should 216 be divided so that the quotient is a perfect square. Also find the square root of the quotient.

Solution :

Expressing 216 as product of prime factors, we get

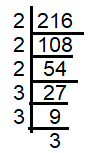
216 = 2 x 2 x 2 x 3 x 3 x 3

By grouping as pairs, we get one 2 and one 3 as extra. So, 216 should be divided by 6 to make it as perfect square.

Dividing 216 by 6, we get 36 as quotient.

√36 = 6