FIND THE INDICATED ANGLE IN THE PARALLELOGRAM WITH DIAGONALS

Find the measure of the indicated angle in each parallelogram.

Example 1 :

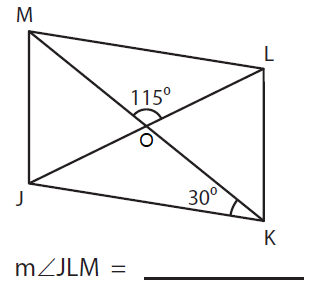
Solution :

In the given figure, ∠JKM = 30° and ∠MOL = 115°

By alternate angles,

∠JKM = ∠KML

30° = ∠KML

In ΔLOM,

We know that,

The sum of the interior angles of a triangle is 180°.

That is,

∠O + ∠M + ∠L = 180°

We have,

 ∠O = 115°, ∠M = 30°, and ∠L = ?

115° + 30° + ∠L = 180°

145° + ∠L = 180°

∠L = 180° - 145°

∠L = 35°

Now, ∠L = 35°. It is similar to m ∠JLM.

So, m ∠JLM = 35°

Example 2 :

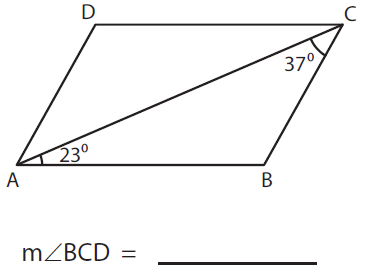
Solution :

In the given figure, ∠BAC = 23° and ∠BCA = 37°

By alternate angles,

∠BAC = ∠ACD

23° = ∠ACD

Now, ∠BCA = 37° and ∠ACD = 23°

To find ∠BCD,

∠BCD = ∠BCA + ∠ACD

= 37° + 23°

∠BCD = 60°

So, m ∠BCD = 60°.

Example 3 :

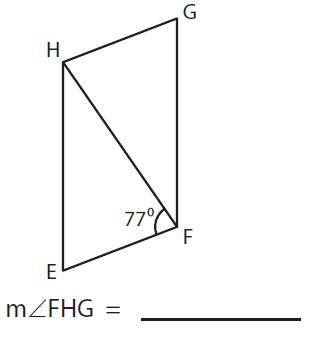
Solution :

In the given figure, ∠EFH = 77°

By alternate angles,

∠EFH = ∠FHG

77° = ∠FHG

So, m ∠FHG = 77°.

Example 4 :

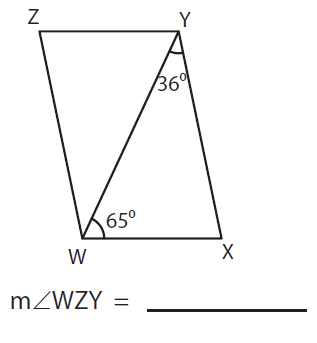
Solution :

In the given figure, ∠XWY = 65° and ∠XYW = 36°

By alternate angles,

In ΔWZY,

The sum of the interior angles of a triangle is 180°.

 ∠YWZ + ∠WYZ + ∠WZY = 180°

We have,

∠YWZ = 36°, ∠WYZ = 65°, and ∠WZY = ?

 36° + 65° + ∠WZY = 180°

101° + ∠WZY = 180°

∠WZY = 180° - 101°

∠WZY = 79°

So, m ∠WZY = 79°.

Example 5 :

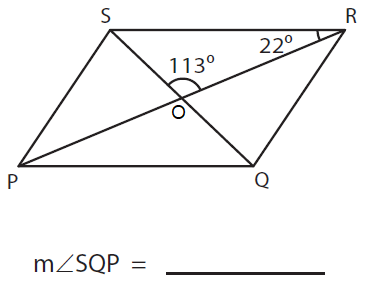
Solution :

In the given figure, ∠PRS = 22° and ∠SOR = 113°

By alternate angles,

∠PRS = ∠RPQ

22° = ∠RPQ = ∠OPQ

By vertically opposite angles,

∠SOR = ∠QOP

113° = ∠QOP

In ΔPOQ,

The sum of the interior angles of a triangle is 180°.

 ∠OPQ + ∠QOP + ∠OQP = 180°

We have,

∠OPQ = 22°, ∠QOP = 113°, and ∠OQP = ?

 22° + 113° + ∠OQP = 180°

135° + ∠OQP = 180°

∠OQP = 180° - 135°

∠OQP = 45° = ∠SQP

So, m ∠SQP = 45°.

Example 6 :

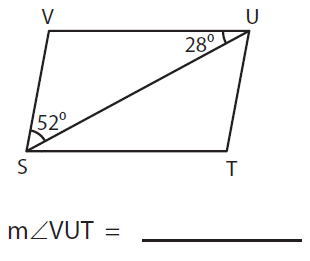
Solution :

In the given figure, ∠VSU = 52° and ∠VUS = 28°

By alternate angles,

∠VUS = ∠UST

28° = ∠UST

To find ∠VUT,

∠VUT = ∠VUS + ∠UST

= 52° + 28°

∠VUT = 80°

So, m ∠VUT = 80°.

Find the value of each variable in the parallelogram.

Example 7 :

Find the indicated measure in ▱LMNQ. Explain your reasoning.

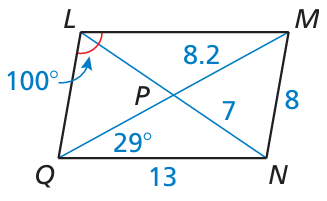
Solution :

a) LM = 13

b)  LP = 7

c) LQ = 8

d) 

MQ = 2(MP)

=  2(8.2)

= 16.4

e) Since LQ and NM are parallel, m∠QLM and m∠LMN co-interior angles.

m∠QLM + m∠LMN = 180

100 + m∠LMN = 180

m∠LMN = 180 - 100

m∠LMN = 80

f)  LM and QN are parallel, then m∠NQL and m∠QLM

m∠NQL + m∠QLM = 180

m∠NQL + 100 = 180

m∠NQL = 180 - 100

= 80

g)  m∠MNQ = 100 (Opposite angles are equal)

h)  m∠LMQ = m∠LMN/2

= 80/2

= 40

Example 8 :

In ▱STUV, m∠TSU = 32°, m∠USV = (x²)°, m∠TUV = 12x°, and ∠TUV is an acute angle. Find m∠USV.

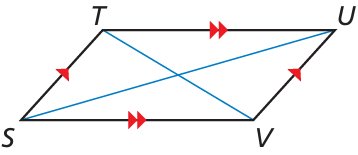
Solution :

m∠TSU = 32°, m∠USV = (x²)°

m∠TSV = m∠TUV (opposite angles are equal)

m∠TSU + m∠USV = m∠TUV

32  + x² = 12x

x² - 12x + 32 = 0

x² - 8x - 4x + 32 = 0

x(x - 8) - 4 (x - 8) = 0

(x - 8) (x - 4) = 0

x = 8 and x = 4

m∠USV = 8² ==> 64

or

m∠USV = 4² ==> 16

Example 9 :

In the diagram of the parking lot shown, m∠JKL = 60°, JK = LM = 21 feet, and KL = JM = 9 feet.

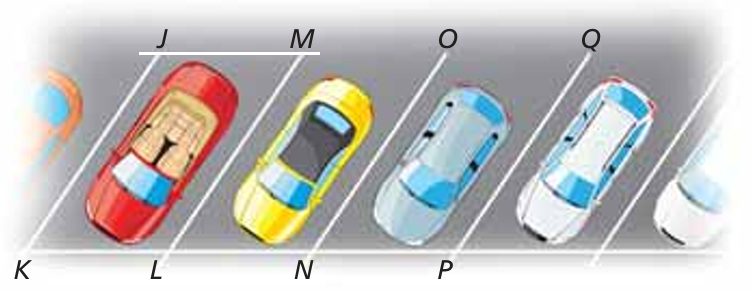
a. Explain how to show that parking space JKLM is a parallelogram.

b. Find m∠JML, m∠KJM, and m∠KLM.

c. LM || NO and NO || PQ . Which theorem could you use to show that JK II PQ ?

Solution :

a)   JK = LM = 21 feet, and KL = JM = 9 feet.

Since opposite sides are equal, then it must be parallelogram.

b) Find m∠JML, m∠KJM, and m∠KLM.

m∠JKL = 60° = m∠JML

m∠JKL + m∠KJM = 180

60 + m∠KJM = 180

m∠KJM = 180 - 60

m∠KJM = 120°

c. Given that LM || NO and NO || PQ, then JK II PQ

Example 10 :

Prove the Parallelogram Opposite Angles Converse. (Hint: Let x ° represent m∠A and m∠C. Let y° represent m∠B and m∠D. Write and simplify an equation involving x and y.) Given ∠A ≅ ∠C, ∠B ≅ ∠D Prove ABCD is a parallelogram.

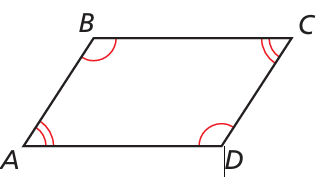
Solution :

Given that,

m∠A = m∠C = x°

m∠B = m∠D = y°

m∠A + m∠B + m∠C + m∠D = 360

m∠A + m∠C + m∠B + m∠D = 360

x + x + y + y = 360

2x + 2y = 360

2(x + y) = 360

x + y = 360/2

x° + y° = 180°

Co-interior angles add upto 180, then the sides AD and BC are parallel. Then ABCD is a parallelogram.