FIND THE HORIZONTAL ASYMPTOTE OF AN EXPONENTIAL FUNCTION

What is horizontal asymptote ?

The horizontal line which is very closer to the curve is known as horizontal asymptote.

Exponential function will be in the form

y = abx - h + k

  • If b > 1, then exponential growth function.
  • If 0 < b < 1, then exponential decay function.

Equation of horizontal asymptote will be y = k

From the graph, to find equation of horizontal asymptote we have to follow the steps below.

  • Observe the graph from bottom to top.
  • The horizontal line which is very closer to the curve is known as horizontal asymptote.

Find the horizontal asymptote of the following exponential functions.

Problem 1 :

y = 2(4/7)x - 4

Solution :

Comparing the given equation with y = abx - h + k

y = k is the equation of horizontal asymptote.

Then, the required horizontal asymptote y = -4

Problem 2 :

Find the equation for the horizontal asymptote of the following function

equation-of-horizontal-asymptote-q1

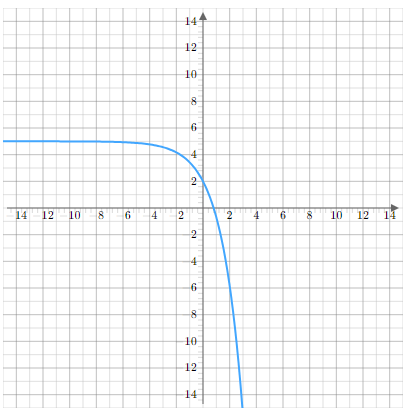
Solution :

While observing the graph from bottom to top, the line drawn at the point y = 5 is closer to the curve. So, equation of horizontal asymptote is y = 5.

Problem 3 :

identify the domain and range for each graphed exponential function.

equation-of-horizontal-asymptote-q2.png

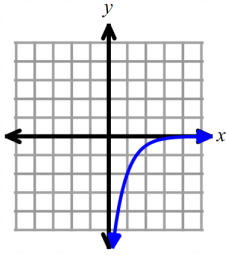
Solution :

To fix domain of the function graphed above, we have to look at the possible outcomes.

So, the domain is all real values.

To fix range of the function, we have to find horizontal asymptote. Here x-axis or y = 0 is closer to the curve.

So, the range is (-∞, 0), the equation of horizontal asymptote is y = 0.

Problem 4 :

identify the domain and range for each graphed exponential function.

equation-of-horizontal-asymptote-q3.png

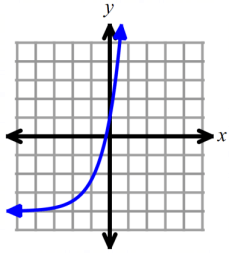
Solution :

To fix domain of the function graphed above, we have to look at the possible outcomes.

So, the domain is all real values.

To fix range of the function, we have to find horizontal asymptote. Here x-axis or y = -4 is closer to the curve.

So, the range is (-4, ∞), the equation of horizontal asymptote is y = -4.

Problem 5 :

identify the domain and range for each graphed exponential function.

equation-of-horizontal-asymptote-q4.png

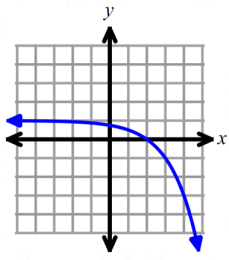
Solution :

To fix domain of the function graphed above, we have to look at the possible outcomes.

So, the domain is all real values.

To fix range of the function, we have to find horizontal asymptote. Here x-axis or y = 1 is closer to the curve.

So, the range is (1, ∞), the equation of horizontal asymptote is y = 1.

Problem 6 :

Find the equation of the horizontal asymptote from the table given below.

equation-of-horizontal-asymptote-q5.png

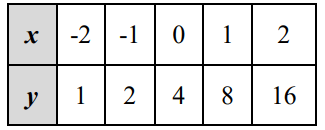
Solution :

To find the equation of horizontal asymptote, we have to find the equation of exponential function.

Choosing two points from the table,

(0, 4) and (1, 8)

y = abx

y = abx

Applying the point (0, 4)

4 = ab0

4 = a(1)

a = 4

Applying the point (1, 8)

8 = ab1

ab = 8

Applying a = 4

b = 8/4

b = 2

By applying the value of a and b, we get

y = 4(2)x

Equation of horizontal asymptote is y = 0.

Problem 7 :

equation-of-horizontal-asymptote-q6.png

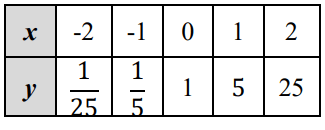
Solution :

To find the equation of horizontal asymptote, we have to find the equation of exponential function.

Choosing two points from the table,

(0, 1) and (1, 5)

y = abx

y = abx

Applying the point (0, 1)

1 = ab0

1 = a(1)

a = 1

Applying the point (1, 5)

5 = ab1

ab = 5

Applying a = 1

b = 5

By applying the value of a and b, we get

y = 1(5)x

Equation of horizontal asymptote is y = 0.

For each exponential function.

  • Complete the table of points.
  • What is the y-intercept?
  • What is the horizontal asymptote of the graph?

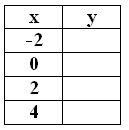
Problem 8 :

y = 2x + 3

equation-of-horizontal-asymptote-q7.png

Solution :

x = -2

y = 2-2+3

y = 1/4 + 3

y = 13/4

x = 0

y = 20+3

y = 1 + 3

y = 4

x = 2

y = 22+3

y = 4+3

y = 7

x = 4

y = 24+3

y = 16+3

y = 19

x

-2

0

2

4

y

13/4

4

7

19

  • y -intercept is 4.
  • Horizontal asymptote is y = 3.

Problem 9 :

y = 2(3)x - 5

equation-of-horizontal-asymptote-q8.png

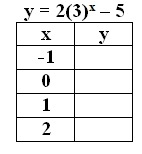
Solution :

x = -2

y = 2-3-5

y = (1/8)-5

y = -39/8

x = 0

y = 20-5

y = 1-5

y = -4

x = 2

y = 22-5

y = 4-5

y = -1

x = 4

y = 2-4-5

y = (1/16)-5

y = -79/16

  • y -intercept is -4.
  • Horizontal asymptote is y = -5.

Problem 10 :

Write the exponential equation in the form y = abx and find horizontal asymptote.

equation-of-horizontal-asymptote-q9.png

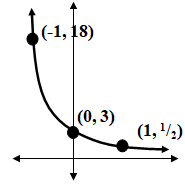
Solution :

Choosing two points from the graph,

(0, 3) and (-1, 18)

y = abx

(0, 3)

3 = ab0

3 = a(1)

a = 3

(-1, 18)

18 = ab-1

18 = a/b

b = 18/3

b = 6

y = 3(6)x

Equation of horizontal asymptote is y = 0.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More