FIND THE HEIGHT OF A CONE GIVEN RADIUS AND SURFACE AREA

What is cone ?

A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.

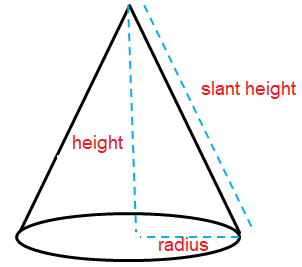
To find lateral surface area and total surface area of cone, we use the formulas given below.

Lateral surface area =  πrl

Total surface area =  πrl +  πr²

= πr(l + r)

l = √r² + h²

Here r = radius, l = slant height

Problem 1 :

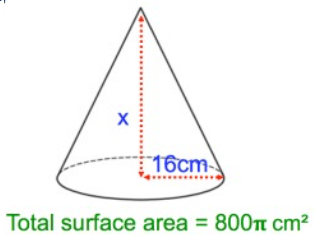
Solution :

Total surface area = 800π

πr(l + r) = 800π

Dividing by π on both sides, we get

r(l + r) = 800 ----(1)

From the given figure, r = 16 cm and h = x

l = √(16² + x²)

Applying the value of l in (1), we get

16(√(16² + x²) + 16) = 800

(√(16² + x²) + 16) = 50

√(16² + x²) = 50 - 16

√(16² + x²) = 34

Take square on both sides.

256 + x² = (34)²

256 + x² = 1156

x² = 1156 - 256

x² = 900

x = 30

Problem 2 :

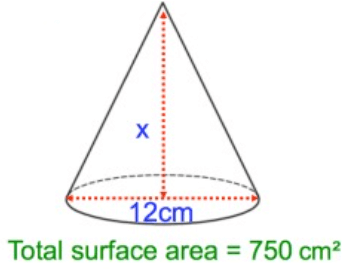
Solution :

Total surface area = 750

πr(l + r) = 750

Here π = 3.14, r = 6

3.14(6)(l + 6) = 750

l + 6 = 750/18.84

l + 6 = 39.80

l = √(6² + x²)

Applying the value of l, we get

√(6² + x²) + 6 = 39.80

√(6² + x²) = 33.80

Take square on both sides.

36 + x² = (33.80)²

36 + x² = 1142.44

x² = 1142.44 - 36

x² = 1106.44

x = 33.26

Problem 3 :

Find what length of canvas 3/4 m wide is required to make a conical tent 8 m in diameter and 3 m in high.

Solution :

Required quantity of canvas = Curved surface area of tent

length x width = πrl

Diameter = 8 m, r = 4 m, height = 3 m

l = √(r² + h²)

slant height (l) = √(4² + 3²)

l = √25

l = 5

length x (3/4) = 3.14(4)(5)

length x (3/4) = 62.8

length = 62.8(4/3)

length = 83.73

So, the required length of the canvas is 83.73 m.

Problem 4 :

Four right circular cylindrical vessels each having diameter 21 cm and height 38 cm are full of ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 7 cm having a hemispherical shape at the top. Find the total number of such cones which can be filled with ice-cream.

Solution :

Quantity of ice creams in four cylinders = Quantity of ice creams in conical shape

Let n be the number of cones to be filled.

4πr²h = n x (1/3)πr²h

4 x (10.5)² x 38 = n x (1/3) x 3.5²x 12

16758 = n x 3.5²x 4

16758 = 49n

n = 16758/49

n = 342

So, the required number of cones is 342.

Problem 5 :

The base radius and height of a right circular solid cone are 2 cm and 8 cm respectively. It is melted and recast into spheres of diameter 2 cm each. Find the number of spheres so formed.

Solution :

Radius of cone = 2 cm, height of cone = 8 cm

Radius of sphere = 1 cm

Let n be the number of spheres to be formed.

Volume of cone = n x volume of sphere

(1/3)πr²h = n x (4/3)πr³

(1/3)r²h = n x (4/3)r³

(1/3) x 2² x 8 = n x (4/3) x 1³

4 x 8 = 4n

n = 32/4

n = 8

So, the required number of spheres is 8.

Problem 6 :

A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 6 cm and its height is 4 cm. find the cost of painting the toy at the rate of $5 per 1000 cm².

Solution :

Radius of cone = 3 cm and height = 4 cm

Area to be painted = surface area of hemisphere + surface area of cone

= 2πr² + πrl 

= π[2r² + rl]------(1)

l² = r² + h²

l² = 3² + 4²

l² = 9 + 16

l² = 25

l = √25

l = 5

Applying these values in (1), we get

= π[2(3²) + 3(5)]

= 3.14[18 + 15]

= 3.14(33)

= 103.62 cm²

Cost of painting = $ 5 per 1000 cm².

1 cm² = 5/1000

= $1/200

The required cost = 103.62(1/200)

= 0.518

Approximately $0.52

Problem 7 :

A corn cob shaped somewhat like a cone has the radius of its broadest end as 2.1 cm and length as 20 cm. If each 1𝑐𝑚² of the surface of the cob carries an average of four grains, find how many grains you would find on the entire cob.

Solution :

Radius = 2.1 cm and height = 20 cm

Surface area of corn cob = πrl 

l² = r² + h²

l² = 2.1² + 20²

= 4.41 + 400

l² = 404.41

l =  √404.41

l = 20.1

= πrl 

= 3.14 x 2.1 x 20.1

= 132.53 cm²

1 cm² = 4 grains

132.53 cm² = 4 x 132.53

= 530.12 corns

Approximately 531 corns.

Problem 8 :

The curved surface area of a cone is 12320 sq. cm, if the radius of its base is 56 cm, then its height is

Solution :

πrl = 12320

radius = 56 cm

3.14 x 56 x l = 12320

l = 12320/(3.14 x 56)

= 70

l² = r² + h²

70² = 56² + h²

h² = 4900 - 3136

h² = 1764

h = √1764

h = 42

So, the required height is 42 cm.