FIND THE FOCUS DIRECTRIX VERTEX AND AXIS OF SYMMETRY FOR THE PARABOLA

Parabola Opens right ward

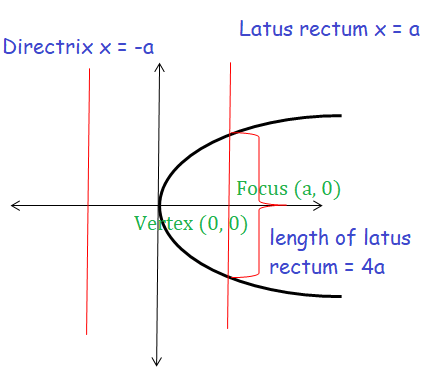
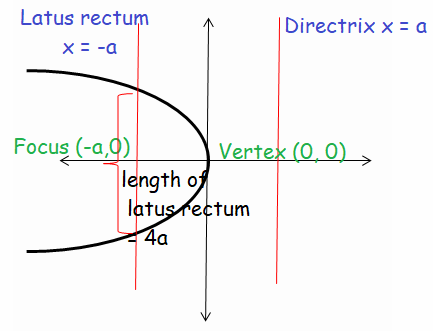
Parabola Opens Left ward

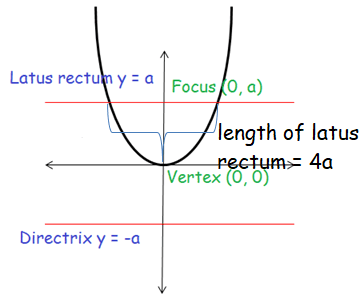
Parabola Opens Up ward

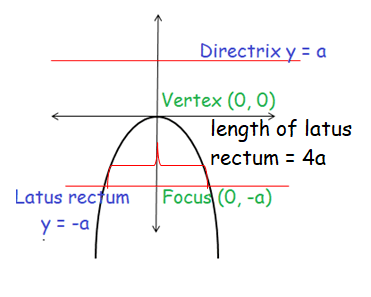
Parabola Opens Down ward

Graph the parabola and identify the vertex, directrix, and focus.

Problem 1 :

y² = -12x

Solution:

y² = -12x

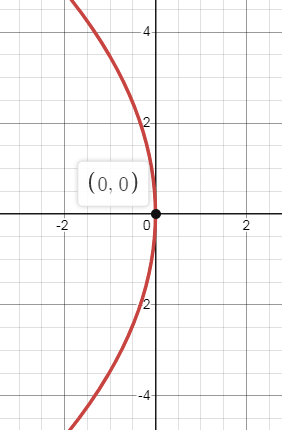
The above equation of parabola is in standard form. The parabola is symmetric about x-axis and it opens to the left.

4a = 12

a = 3

Vertex:

(0, 0)

Equation of directrix:

x = a

x = 3

Focus:

F(-a, 0) = F(-3, 0)

Problem 2 :

x² = 8y

Solution:

x² = 8y

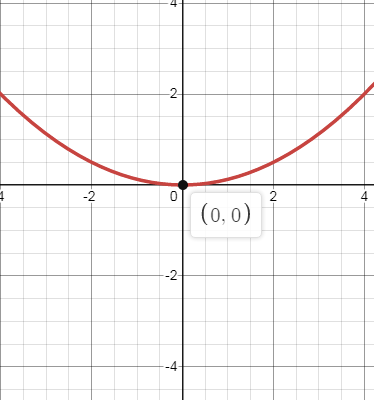
The above equation of parabola is in standard form. The parabola is symmetric about y-axis and it opens to the up.

4a = 8

a = 2

Vertex:

(0, 0)

Equation of directrix:

y = -a

y = -2

Focus:

F(0, a) = F(0, 2)

Problem 3 :

6(x + 1)² + 12(y - 3) = 0

Solution:

6(x + 1)² + 12(y - 3) = 0

6(x + 1)² = -12(y - 3)

(x + 1)² = -12/6 (y - 3)

(x + 1)² = -2(y - 3)

Let X = x + 1 and Y = y - 3

X² = -2Y

The above equation of parabola is in standard form. The parabola is symmetric about y-axis and it opens to the down.

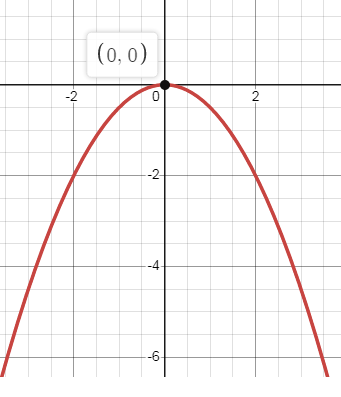
4a = 2

a = 1/2

Vertex :

(0, 0)

X = 0 and Y = 0

x + 1 = 0 and y - 3 = 0

x = -1 and y = 3

The vertex is (-1, 3).

Equation of directrix:

Y = a

Y = 1/2

Y = 0.5

y - 3 = 0.5

y = 0.5 + 3

y = 3.5

Focus:

F(0, -a) = F(0, -0.5)

X = 0 and Y = -0.5

x + 1 = 0 and y - 3 = -0.5

x = -1 and y = 2.5

The focus is (-1, 2.5).

Problem 4 :

y² - 12(x + 2) = 0

Solution:

y² - 12(x + 2) = 0

y² = 12(x + 2)

Let X = x + 2

y² = 12X

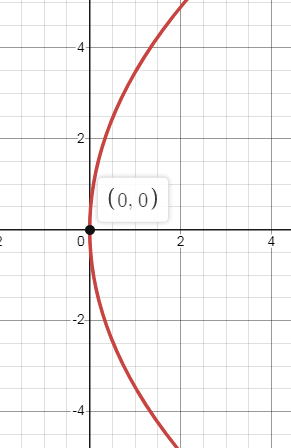
The above equation of parabola is in standard form. The parabola is symmetric about x-axis and it opens to the left.

4a = 12

a = 3

Vertex:

(0, 0)

X = 0 and Y = 0

x + 2 = 0 and y = 0

x = -2 and y = 0

The vertex is (-2, 0).

Equation of directrix:

X = -a

X = -3

x + 2 = -3

x = -5

Focus:

F(a, 0) = F(3, 0)

x + 2 = 3

x = 1

The focus is (1, 0).

Problem 5 :

(x + 2)² = -8(y + 2)

Solution:

(x + 2)² = -8(y + 2)

Let X = x + 2 and Y = y + 2

X² = -8Y

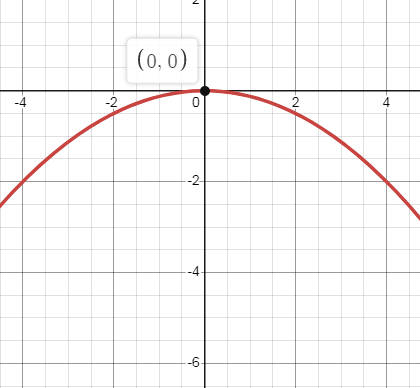
The above equation of parabola is in standard form. The parabola is symmetric about y-axis and it opens to the down.

4a = 8

a = 2

Vertex:

(0, 0)

X = 0 and Y = 0

x + 2 = 0 and y + 2 = 0

x = -2 and y = -2

The vertex is (-2, -2).

Equation of directrix:

Y = a

Y = 2

y + 2 = 2

y  = 0

Focus:

F(0, -a) = F(0, -2)

X = 0 and Y = -2

x + 2 = 0 and y + 2 = -2

x = -2 and y = -4

The focus is (-2, -4).

Problem 6 :

(y - 1)² = -8x

Solution:

(y - 1)² = -8x

Let Y = y - 1

Y² = -8x 

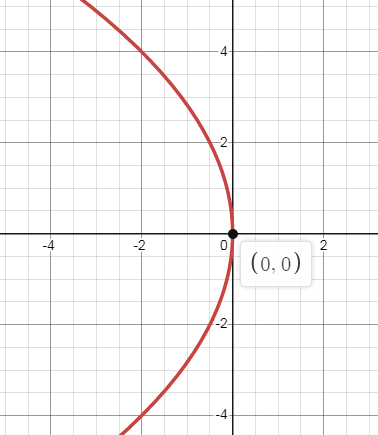
The above equation of parabola is in standard form. The parabola is symmetric about x-axis and it opens to the left.

4a = 8

a = 2

Vertex:

(0, 0)

Y = 0

y - 1 = 0

y = 1

The vertex is (0, 1).

Equation of directrix:

x = a

x = 2

Focus:

F(-a, 0) = F(-2, 0)

x = -2 and Y = 0

 y - 1 = 0

x = -2 and y = 1

The focus is (-2, 1).