FIND THE EQUATION OF THE IMAGE LINE UNDER THE ROTATION OF GIVEN ANGLE

When (x, y) moves under a rotation about O through an angle of θ to a new position P'(x', y'), then OP = OP' and POP' = θ where positive θ is measured anticlockwise.

O is the only point which does not move under the rotation.

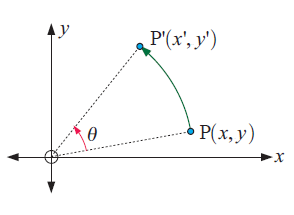
R_θ means a rotation about O through an angle of θ⁰

Original point (x, y) (x, y) (x, y)

Angle rotation 90 degree -90 degree 180 degree

Image (-y, x) (y, -x) (-x, -y)

Problem 1 :

Find the image equation of the line 2x - 3y = -6 under clockwise rotation about O through 90°.

Solution :

Given line is 2x - 3y = -6

Angle rotation to be performed = 90°clockwise rotation.

Rule to be applied :

(x, y) ==> (-y, x)

2(-y) - 3x = -6

-2y - 3x = -6

Multiplying by the negative sign through out the equation, we get

3x + 2y = 6

Problem 2 :

Find the image of the equation when 3x - 4y  = 7 is rotated clockwise through a quarter turn about O.

Solution :

Given line is 3x - 4y  = 7

Angle rotation to be performed = quarter turn clockwise rotation.

That is, 90°clockwise rotation.

Rule to be applied :

(x, y) ==> (-y, x)

3(-y) - 4x  = 7

-3y - 4x = 7

Multiplying by the negative sign, we get

4x + 3y = -7

Problem 3 :

Find the image of the equation when y = -3 is rotated anticlockwise through 90° about O.

Solution :

Given line is y = -3

Angle rotation to be performed = 90° counter clockwise rotation.

Rule to be applied :

(x, y) ==> (y, -x)

-x = -3

Ignoring negative sign on both sides, we get 

x = 3

Problem 4 :

Find the image of the equation when x = 7 is rotated  through 180° about O.

Solution :

Given line is x = 7

Angle rotation to be performed = 180° 

Rule to be applied :

(x, y) ==> (-x, -y)

-x = 7

Multiplying by negative on both sides, we get

x = -7

then x + 7 = 0

Problem 5 :

Find the image of the equation when y = x² is rotated  through 180° about O.

Solution :

Given curve is y = x²

Angle rotation to be performed = 180° 

Rule to be applied :

(x, y) ==> (-x, -y)

-y = (-x)²

-y = x²

Multiplying by negative on both sides, we get

y = -x²

Problem 6 :

Find the image of the equation when 2x + 3y = 12 is rotated  clockwise direction through 90° about O.

Solution :

Given line is 2x + 3y = 12 

Angle rotation to be performed = 90° clockwise rotation

Rule to be applied :

(x, y) ==> (-y, x)

2(-y) + 3x = 12 

3x - 2y = 12

Problem 7 :

Find the image of the line x - y = 8 under M _{y = -x} followed by the translation (4, -1).

Solution :

x - y = 8

Reflection across the line y = -x, to perform this we have to follow the rule,

(x, y) ==> change x as -y and change y as -x

In the given line doing the above changes,

-y - (-x) = 8

x - y = 8 after the reflection.

After the translation :

Moving 4 units right and 1 unit down.

x' = x + 4 and y' = y - 1

x + 4 - (y - 1) = 8

x + 4 - y + 1 = 8

x - y + 5 = 8

x - y = 8 - 5

x - y = 3

Problem 8 :

Find the image of the line x + 2y = -4 under R _-90 followed by the translation (2, -5).

Solution :

x + 2y = -4

Rotation of 90 degree in anticlockwise direction. To perform this, we have to follow the rule

(x, y) ==> (y, -x)

In the given line doing the above changes,

y + 2(-x) = -4

-2x + y = -4

After the translation :

Moving 2 units right and 5 units down.

x' = x + 2 and y' = y - 5

-2(x + 2) + y - 5 = -4

-2x - 4 + y - 5 = -4

-2x + y - 9 = -4

-2x + y = -4 + 9

-2x + y = 5

Multiplying by negative through out the equation, we get

2x - y = -5

Problem 9 :

Find the image of the line x + y = 1 under M ₉₀ followed by M _{y = x} followed by the translation (3, 1).

Solution :

90 degree clockwise rotation :

(x, y) --> (-y, x)

-y + x = 1

x - y = 1

Reflection across y = x :

x - y = 1

To perform the reflection across y = x, we have to follow the rule given below.

x should be changed as y and y should be changed as x

y - x = 1

-x + y = 1

After the translation :

Moving 3 units right and 1 unit up

x' = x + 3 and y' = y + 1

-(x + 3 )+ y + 1 = 1

-x + y - 3 + 1 = 1

-x + y - 2 = 1

-x + y = 3

y = x + 3

x + y = 1 - 2

x + y = -1