FIND EQUATION OF THE IMAGE LINE UNDER REFLECTION

When P(x, y) is reflected in the mirror line to become P(x', y')  the mirror line perpendicularly bisects [pp]'

Thus every point on an object, the mirror line perpendicularly bisects the line segment joining the point with its image.

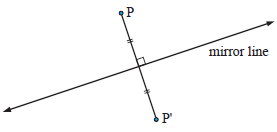
• M_x the reflection in the x-axis.
• M_y the reflection in the y-axis.
• M_{y = x} the reflection in the line y = x
• M_{y = -x} the reflection in the line y = -x

Reflection in the x-axis Reflection in the y-axis Reflection in the line y = x Reflection in the line y = -x

(x, y) --> (x, -y) (x, y) --> (-x, y) (x, y) --> (y, x) (x, y) --> (-y, -x)

Problem 1 :

Find the image equation of 2x - 3y = 8 reflected in the y-axis.

Solution :

Reflection in the y-axis :

Rule to be applied :

x should be changed as -x, y will be the same.

2(-x) - 3y = 8

-2x - 3y = 8

Multiplying by negative, we get

2x + 3y = -8

Problem 2 :

Find the image equation of y = 2x +3 under M_x

Solution :

Reflection under the x-axis :

Rule to be applied :

y should be changed as -y, x will be the same.

-y = 2x +3

2x + y + 3 = 0

or

y = -2x - 3

Problem 3 :

Find the image equation of y = x² under M_x

Solution :

Reflection under the x-axis :

Rule to be applied :

y should be changed as -y, x will be the same.

-y = x²

y = -x²

Problem 4 :

Find the image equation of y = 2^x under M_{y = x}

Solution :

Reflection under the x-axis :

Rule to be applied :

Change x as y and change y as x.

x = 2^y

Problem 5 :

Find the image equation of 2x + 3y = 4 under M_{y = -x}

Solution :

Reflection under the line y = -x :

Rule to be applied :

Change x as -y and change y as -x.

2(-y) + 3(-x) = 4

-2y - 3x = 4

Multiplying by negative sign, we get

3x + 2y = -4

Problem 6 :

Find the image equation of x = 3 under M_{y = -x}

Solution :

Reflection under the line y = -x :

Rule to be applied :

Change x as -y and change y as -x.

-y = 3

y = -3

Problem 7 :

Find the image equation of y = 2x² under M_{y = x}

Solution :

Reflection under the line y = x :

Rule to be applied :

Change x as y and change y as x.

x = 2y²

Problem 8 :

Find the image equation of y = 5/x under M_{y = x}

Solution :

Reflection under the line y = x :

Rule to be applied :

Change x as y and change y as x.

x = 5/y