FIND THE EQUATION OF A TRANSFORMED EXPONENTIAL FUNCTION FROM A GRAPH

Find the exponential function represented by the graph given below.

Problem 1 :

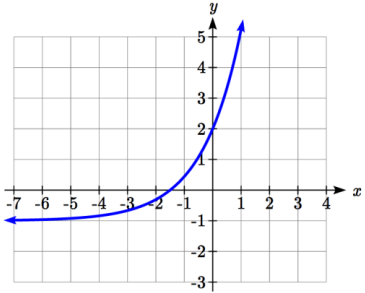
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = -1. So, k = -1

y = ab^x - 1 ------(1)

Tracing two points from the graph of the given function given above.

(0, 2) and (-5, -1)

Applying the point (0, 2) in (1), we get

2 = ab⁰ - 1

2 = a(1) - 1

a = 2 + 1

a = 3

Applying the point (1, 5) in (1), we get

5 = ab¹ - 1

6 = 3(b¹)

b = 6/3

b = 2

So, the required exponential function is

y = 3(2)^x - 1

Problem 2 :

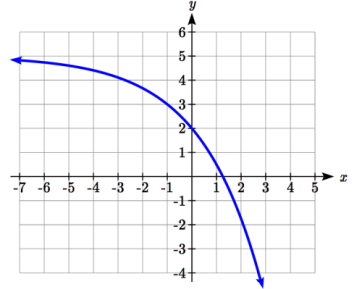
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 5. So, k = 5

y = ab^x + 5 ------(1)

Tracing two points from the graph of the given function given above.

 (0, 2) and (-1, 3)

Applying the point (0, 2) in (1), we get

2 = ab⁰ + 5

2 - 5 = a(1)

a = -3

Applying the point (-1, 3) in (1), we get

3 = (-3)b^-1 + 5

3 - 5 = -3(1/b)

-2 = -3/b

b = 3/2

b = 1.5

So, the required exponential function is

y = -3(1.5)^x + 5

Problem 3 :

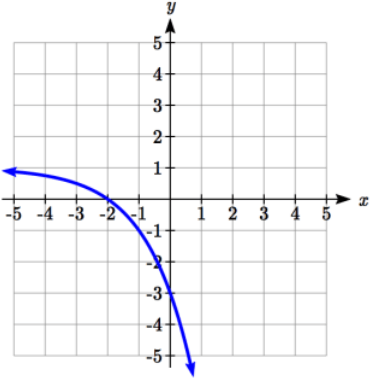
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 1. So, k = 1

y = ab^x + 1 ------(1)

Tracing two points from the graph of the given function given above.

 (-2, 0) and (0, -3)

Applying the point (-2, 0) in (1), we get

0 = ab^-2 + 1

-1 = a/b²

Applying the point (0, -3) in (1), we get

-3 = ab⁰ + 1

-3 - 1 = a(1)

a = -4

Applying the value of a, we get

-4/b² = -1

b² = 4

b = 2

So, the required exponential function is

y = -4(1.5)^x + 5

Problem 4 :

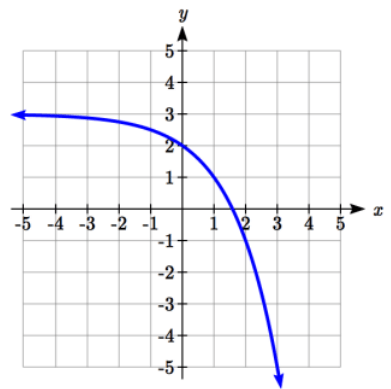
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 3. So, k = 3

y = ab^x + 3 ------(1)

Tracing two points from the graph of the given function given above.

 (0, 2) and (1, 1)

Applying the point (0, 2) in (1), we get

2 = ab⁰ + 3

-1 = a(1)

a = -1

Applying the point (1, 1) in (1), we get

1 = (-1)b¹ + 3

1 - 3 = -b

b = 2

So, the required exponential function is

y = -1(2)^x + 3

Problem 5 :

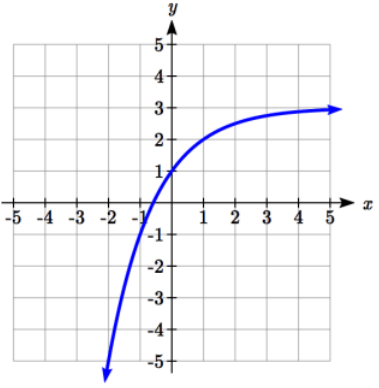
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 3. So, k = 3

y = ab^x + 3 ------(1)

Tracing two points from the graph of the given function given above.

 (0, 1) and (-1, -1)

Applying the point (0, 1) in (1), we get

1 = ab⁰ + 3

-2 = a(1)

a = -2

Applying the point (-1, -1) in (1), we get

-1 = (-2)b^-1 + 3

-4/(-2) = 1/b

b = 1/2

So, the required exponential function is

y = -2(1/2)^x + 3

Problem 6 :

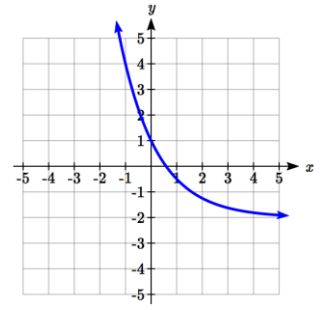
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = -2. So, k = -2

y = ab^x - 2------(1)

Tracing two points from the graph of the given function given above.

 (0, 1) and (-1, 4)

Applying the point (0, 1) in (1), we get

1 = ab⁰ - 2

3 = a(1)

a = 3

Applying the point (-1, 4) in (1), we get

4 = (2)b^-1 - 2

4 + 2 = 2/b

6b = 2

b = 1/3

So, the required exponential function is

y = 3(1/3)^x - 2

Problem 7 :

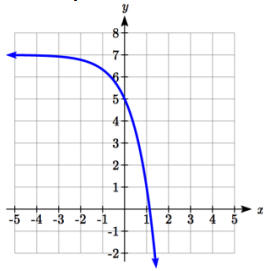
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 7. So, k = 7

y = ab^x + 7------(1)

Tracing two points from the graph of the given function given above.

 (0, 5) and (1, 1)

Applying the point (0, 5) in (1), we get

5 = ab⁰ + 7

5 - 7 = a(1)

a = -2

Applying the point (1, 1) in (1), we get

1 = (-2)b¹ + 7

-6 = -2b

b = 3

So, the required exponential function is

y = -2(3)^x + 7

Problem 8 :

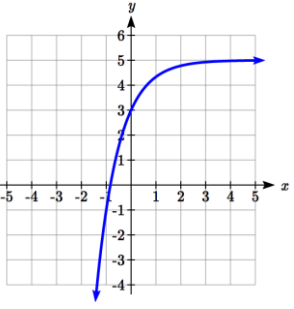
Solution :

y = ab^x + k

Here, the Horizontal asymptote is y = 5. So, k = 5

y = ab^x + 5------(1)

Tracing two points from the graph of the given function given above.

 (0, 3) and (-1, -1)

Applying the point (0, 3) in (1), we get

3 = ab⁰ + 5

-2 = a(1)

a = -2

Applying the point (-1, -1) in (1), we get

-1 = (-2)b^-1 + 5

-6 = -2/b

b = 1/3

So, the required exponential function is

y = -2(1/3)^x + 5