FIND THE AREA OF SHADED COMPOSITE FIGURES

Work out the shaded area.

Problem 1 :

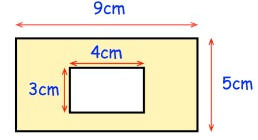
Solution :

Shaded area = Area of large rectangle – area of small rectangle

= (9 × 5) – (4 × 3)

= 45 – 12

= 33 cm²

So, shaded area is 33 cm².

Problem 2 :

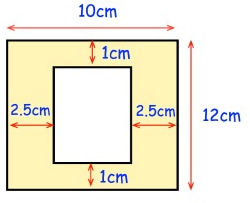
Solution :

Shaded area

= Area of large rectangle - area of small rectangle

length of large rectangle = 10 cm, width = 12 cm

length of small rectangle = 10 - 2.5 - 2.5 ==> 5 cm

Width of the small rectangle = 12 - 1 - 1 ==> 10 cm

= (10 x 12) - (5 x 10)

= 120 - 50

= 70 cm²

Problem 3 :

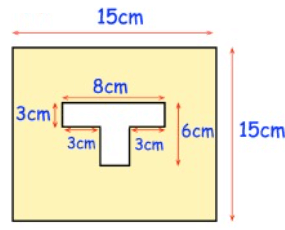
Solution :

Shaded area

= Area of square – Area of large rectangle - Area of small rectangle

= (15)² – (8 × 3) – (2 × 3)

= 225 – 24 – 6

= 195 cm²

So, shaded area is 195 cm².

Shown is a triangular brick wall with a rectangular window. Find the area of the wall that is brick.

Problem 4 :

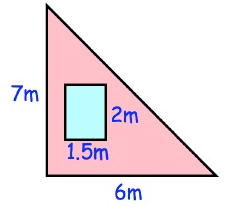
Solution :

Area of the wall = area of a triangle – area of rectangle

= (1/2) (b × h) - (l × w)

= (1/2) (6 × 7) – (1.5 × 2)

= 1/2 (42) – 3

= 21 – 3

= 18 m²

So, area of the wall is 18 m².

Find the area of the garden that is grass.

Problem 5 :

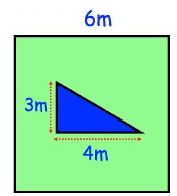
Solution :

The area of the garden = area of square - area of triangle

= a² – 1/2 (b × h)

= 6² – 1/2 (4 × 3)

= 36 – 1/2 (12)

= 36 – 6

= 30 m²

So, area of the garden is 30 m².

Problem 6 :

You are deciding on two different designs for envelopes.

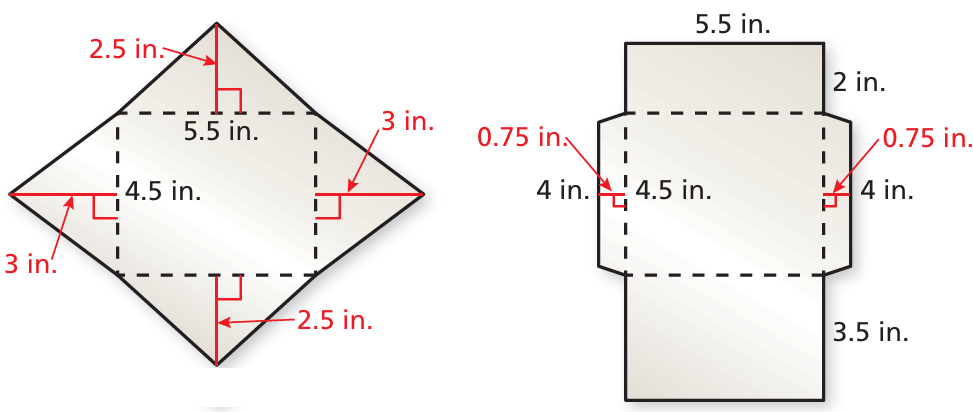
a. Which design has the greater area?

b. You make 500 envelopes using the design with the greater area. Using the same amount of paper, how many more envelopes can you make with the other design?

Solution :

a) 

Area of the first envelop = area of rectangle + 4(area of triangle)

= 4.5 x 5.5 + 4(1/2) x 4.5 x 3

= 24.75  2 x 4.5 x 3

= 24.75 + 27

= 51.75 square inches.

Area of the second envelop = Area of rectangle in the middle + 2(area of rectangles in the top and bottom) + 2(area of trapezium to the right and left)

= 4.5 x 5.5 + 2(5.5 x 2) + 2(1/2) x 0.75 x (4 + 4.5)

= 24.75 + 22 + 6.375

= 53.125 square inches

So, the second envelop has greater area.

b)

Area created with 500 envelops = 500 x 53.125

= 26562.5 square inches

Number of envelops can be made with other desgin = 26562.5/51.75

= 513.28

Approximately 513 envelops.

Problem 7 :

Find the area of the figure.

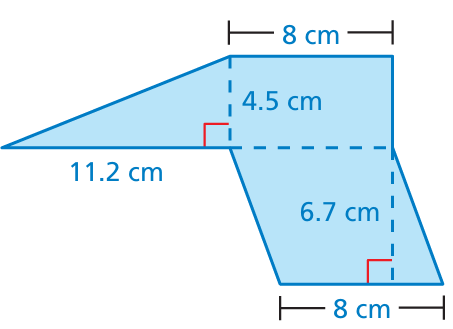
Solution :

Area of the shape above = Area of rectangle + area of triangle + area of parallelogram

= 8 x 4.5 + (1/2) x 4.5 x 11.2 + 8 x 6.7

= 36 + 25.2 + 53.6

= 114.8 cm²

Find the area of the figure.

Problem 8 :

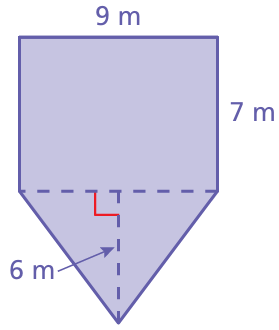
Solution :

Area of shape above = area of triangle + area of rectangle

= 1/2 x 9 x 6 + 9 x 7

= 9 x 3 + 63

= 27 + 63

= 90 m²

Problem 9 :

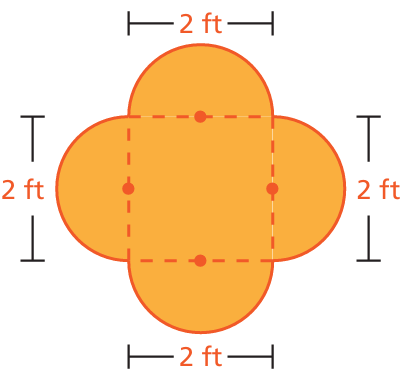
Solution :

Area of the shape given = area of square + 4(area of semi circle)

= 2 x 2 + 4(1/2)πr²

= 4 + 2 x 3.14 x 1²

= 4 + 6.28

= 10.28 square ft

Problem 10 :

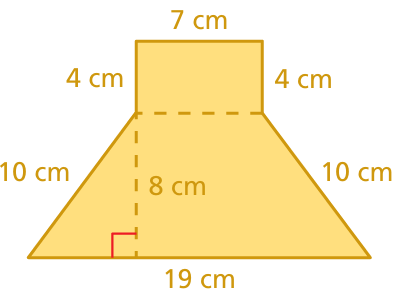
Solution :

Area of the shape above = area of trapezium + area of rectangle

= 1/2 x 8 (19 + 7) + 7 x 4

= 4 x 26 + 28

= 104 + 28

= 132 square cm

Problem 11 :

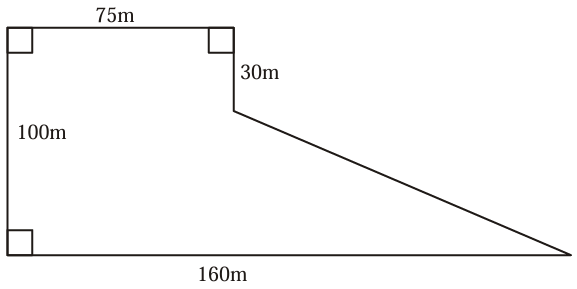
The diagram shows the plan of a field. The farmer sells the field for £3 per square metre. Work out the total amount of money the farmer should get.

Solution :

Area of the shape given = Area of rectangle to the left + area of triangle to the right

= length x width + (1/2) x base x height

Height of the triangle = 160 - 75

= 85 m

= 75 x 100 + (1/2) x 100 x 85

= 7500 + 50 x 85

= 7500 + 4250

= 11750 square meter

Area of the field = £3 per square

Total cost = 3 x 11750

= £35250

Problem 12 :

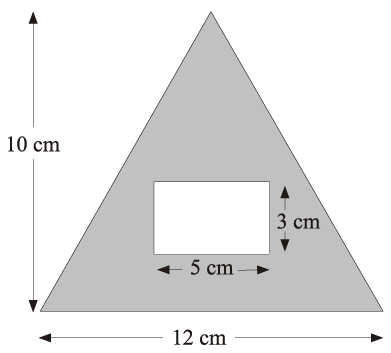
The diagram shows a rectangle inside a triangle. The triangle has a base of 12 cm and a height of 10 cm. The rectangle is 5 cm by 3 cm. Work out the area of the region shown shaded in the diagram.

Solution :

Area of shaded region = area of triangle - area of rectangle

= (1/2) x 12 x 10 - 5 x 3

= 60 - 15

= 45 cm²

Problem 13 :

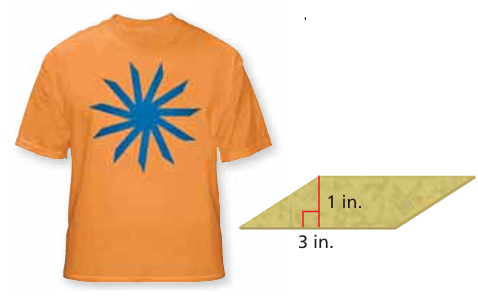
You use the parallelogram-shaped sponge to create the T-shirt design. The area of the design is 66 square inches. How many times do you use the sponge to create the design? Draw a diagram to support your answer.

Solution :

Area of design = 66 square inches

The sponge is in the shape of parallelogram, then its area

= base x height

= 3 x 1

= 3 square inches

In the design, the shape parallelogram is repeating 11 times,

Number of times to use the sponge to create the design

= Area of design ÷ Area of parallelogram-shaped sponge

= 66 square inches ÷ 3 square inches

= 22 Times

Therefore,

The sponge can be used 22 times to create the design.