FIND THE AMPLITUDE PERIOD AND PHASE SHIFT OF A TRIGONOMETRIC FUNCTION

Problem 1 :

State the period, amplitude, horizontal translation, and equation of the axis for each of the following trigonometric functions

a) 0.5 cos (4x)

b) y = 2 cos (3x) - 1

c) y = sin (x - π/4) + 3

d) y = 5 cos (-2x + π/3) - 2

Solution :

a) 0.5 cos (4x)

a = 0.5, k = 4, d = 0 and c = 0

Amplitude :

Amplitude = |0.5|

= 0.5

Period :

Period = 2π/|k|

= 2π/4

= π/2

Horizontal translation :

There is no horizontal translation.

Equation of axis : 

x-axis or y = 0

b) y = 2 cos (3x) - 1

a = 2, k = 3, d = 0 and c = -1

Amplitude :

Amplitude = |2|

= 2

Period :

Period = 2π/|k|

= 2π/3

Horizontal translation :

There is no horizontal translation.

Equation of axis : 

y = -1

c) y = sin (x - π/4) + 3

a = 1, k = 1, d = π/4 and c = 3

Amplitude :

Amplitude = |1|

= 1

Period :

Period = 2π/|k|

= 2π/1

= 2π

Horizontal translation :

π/4

Equation of axis : 

y = 3

d) y = 5 cos (-2x + π/3) - 2

y = 5 cos (-2(x - π/6)) - 2

a = 5, k = -2, d = π/6 and c = -2

Amplitude :

Amplitude = |5|

= 5

Period :

Period = 2π/|k|

= 2π/|-2|

= π

Horizontal translation :

π/6

Equation of axis : 

y = -2

Problem 2 :

The following trigonometric functions have the parent function

f(x) = sin x

They have undergone no horizontal translations and no reflections in either axis. Determine the equation of each function.

a) The graph of this trigonometric function has a period of  π and an amplitude of 25. The equation of the axis y = -4

b) The graph of this trigonometric function has a period of 10 and an amplitude of  2/5 the equation of the axis is y = 1/15

c) The graph of this trigonometric function has a period of 6π and an amplitude of 80. The equation of the axis is y = -9/10

d) The graph of this trigonometric function has a period of 1/2 and an amplitude of 11. The equation of the axis is y = 0

Solution :

a)

Period = π

Amplitude = 25

equation of the axis y = -4

y = a sin (k(x - d)) + c

a = 25

period = 2π/|k|

π = 2π/|k|

|k| = 2π/π

k = 2

Horizontal shift = 0

c = -4

y = 25 sin (2x) - 4

So, the required function is y = 25 sin (2x) - 4.

b) 

Period = 10

Amplitude = 2/5

equation of the axis y = 1/15

y = a sin (k(x - d)) + c

a = 2/5

period = 2π/|k|

10 = 2π/|k|

|k| = 2π/10

k = π/5

Horizontal shift = 0

c = 1/15

y = 2/5 sin (πx/5) + 1/15

So, the required function is y = 2/5 sin (πx/5) + 1/15

c) 

Period = 6π

Amplitude = 80

equation of the axis y = -9/10

y = a sin (k(x - d)) + c

a = 80

period = 2π/|k|

6π = 2π/|k|

|k| = 2π/6π

k = 1/3

Horizontal shift = 0

c = -9/10

y = 80 sin (x/3) - 9/10

So, the required function is y = 80 sin (x/3) - 9/10

d) 

Period = 1/2

Amplitude = 11

equation of the axis y = 0

y = a sin (k(x - d)) + c

a = 11

period = 2π/|k|

11 = 2π/|k|

|k| = 2π/11

k = 2π/11

Horizontal shift = 0

c = 0

y = 11 sin (2πx/11) - 0

So, the required function is y = 11 sin (2πx/11).

Problem 3 :

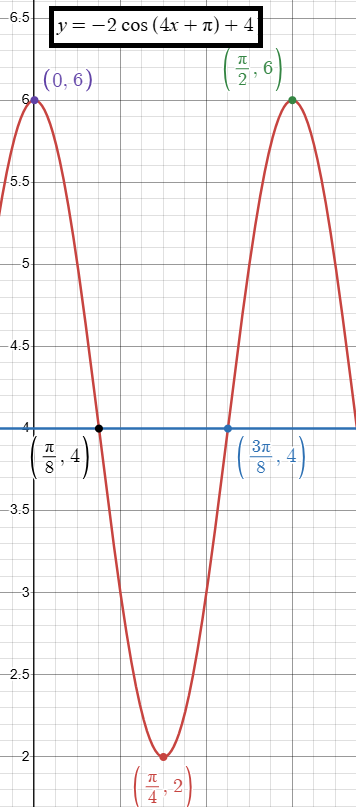
Identify the key characteristics of y = -2 cos (4x + π) + 4 and sketch the graph.

Solution :

y = -2 cos (4x + π) + 4

y = -2 cos (4(x + π/4)) + 4

y = -2 cos (4(x - (-π/4)) + 4

Comparing the given function with y = a cos(k(x - d)) + c

a = -2 (it is reflection across the x-axis)

a = |-2| = 2

k = 4, d = -π/4 and c = 4

Period = 2π/|k|

Period = 2π/4

= π/2

Horizontal shift of π/4 to the left and equation of axis is y = 4

Inputs are 

0, π/8, 2π/8, 3π/8, 4π/8

0, π/8, π/4, 3π/8, π/2

Maximum value = 6

Minimum value = 2

(0, 6) (π/8, 4)(π/4, 2)(3π/8, 4) (π/2, 6)

Problem 4 :

Each person's blood pressure is different but there is range of blood pressure values that is considered healthy. The function

P(t) = -20 cos (5π/3) t + 100

models the blood pressure, p, in millimeters of mercury, at time t, in seconds, of a person at rest.

a) What is the period of the function? What does the period represent for an individual?

b) How many times does this person’s heart beat each minute?

c) Sketch the graph of y = P(t) for 0 ≤ t ≤ 6

d) What is the range of the function? Explain the meaning of the range in terms of a person’s blood pressure.

Solution :

P(t) = -20 cos (5π/3) t + 100

Comparing the given function with 

y = a cos(k(x - d)) + c

a = 20, k = 5π/3, d = 0 and c = 100

a) Period = 2 π / |k|

= 2 π / (5π/3)

= 6/5

= 1.2 seconds

This represents the time between one beat of a person’s heart and the next beat.

b) 1 heart beat in 1.2 seconds. 

1 minute = 60 seconds

1 : 1.2 = x : 60

1/1.2 = x/60

x = 60/1.2

= 50 heart beats

c) 

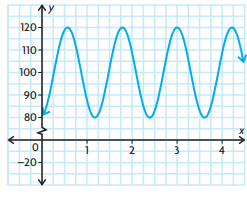
d) The range for the function is between 80 and 120. The range means the lowest blood pressure is 80 and the highest blood pressure is 120