FIND THE ALTITUDE OF EQUILATERAL TRIANGLE FROM THE GIVEN PERIMETER

Problem 1 :

The perimeter of an equilateral triangle is 24. What is the length of each altitude of the triangle ?

A) 4√3      B) 8√3   C) 4    D) 16

Solution :

Let ‘a’ be the side length of the equilateral triangle.

Perimeter of equilateral triangle = 24

3a = 24

a = 24/3

a = 8

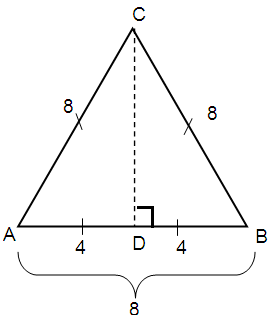
By using Pythagorean theorem

AC² = AD² + DC²

8² = 4² + DC²

64 = 16 + DC²

DC² = 64 - 16

DC² = 48

DC = √48

= √(16 × 3)

= √(4 × 4 × 3)

= 4√3

So, the length of each altitude of the triangle = 4√3

So, option A) is correct.

Problem 2 :

The perimeter of an equilateral triangle is 12. What is the length of each altitude of the triangle ?

A) 2       B) 4√3       C) 2√3       D) 8

Solution :

Let ‘a’ be the side length of the equilateral triangle.

Perimeter of equilateral triangle = 12

3a = 12

a = 12/3

a = 4

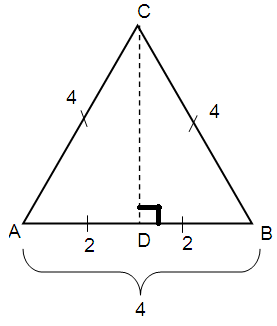
By using Pythagorean theorem

AC² = AD² + DC²

4² = 2² + DC²

16 = 4 + DC²

DC² = 16 - 4

DC² = 12

DC = √12

= 2√3

So, the length of each altitude of the triangle = 2√3

So, option C) is correct.

Problem 3 :

The perimeter of an equilateral triangle is 18. What is the length of each altitude of the triangle ?

A) 6     B) 3√3   C) 6√3     D) 12

Solution :

Let ‘a’ be the side length of the equilateral triangle.

Perimeter of equilateral triangle = 18

So, 3a = 18

a = 18/3

a = 6

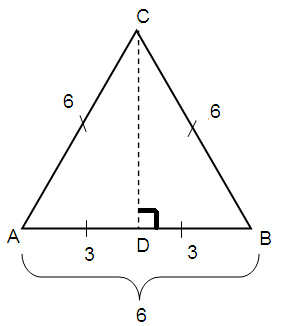
By using Pythagorean theorem

AC² = AD² + DC²

6² = 3² + DC²

36 = 9 + DC²

DC² = 36 - 9

DC² = 27

DC = √27

= 3√3

So, the length of each altitude of the triangle = 3√3

So, option B) is correct.

Problem 4 :

The perimeter of an equilateral triangle measures 30 cm. What is the length of the altitude?

A) 10√3       B) 5√3      C) 5       D) 5√2

Solution :

Let ‘a’ be the side length of the equilateral triangle.

Perimeter of equilateral triangle = 30 cm

So, 3a = 30

a = 30/3

a = 10

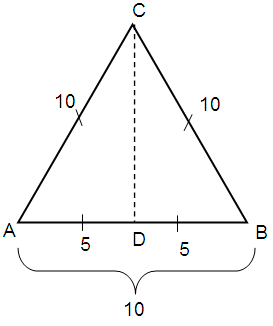
By using Pythagorean theorem

AC² = AD² + DC²

10² = 5² + DC²

100 = 25 + DC²

DC² = 100 - 25

DC² = 75

DC = √75

= 5√3

Length of each altitude of the triangle = 5√3.

So, option B) is correct.