FIND SLANT HEIGHT OF CONE GIVEN SURFACE AREA AND RADIUS

Find slant height of the following cones given below.

Problem 1 :

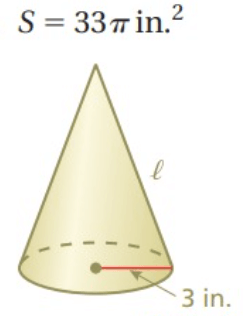
Solution :

Total surface area = πr(l + r)

πr(l + r) = 33π

radius(r) = 3

3π(l + 3) = 33π

3(l + 3) = 11

Subtracting 3 on both sides.

l = 11 - 3

l = 8

So, the required slant height is 8 inches.

Problem 2 :

Solution :

Total surface area = πr(l + r)

πr(l + r) = 126π

diameter = 12 cm

radius(r) = 6 cm

6π(l + 6) = 126π

6(l + 6) = 126

Dividing by 6 on both sides.

l + 6 = 21

Subtracting 6 on both sides.

l = 21 - 6

l = 15

So, the required slant height is 15 cm.

Problem 3 :

Solution :

Total surface area = πr(l + r)

πr(l + r) = 60π

radius(r) = 5 ft

5π(l + 5) = 60π

5(l + 5) = 60

Dividing by 5 on both sides.

l + 5 = 12

Subtracting 5 on both sides.

l = 12 - 5

l = 7

So, the required slant height is 7 ft.

Problem 4 :

Solution :

Total surface area = πr(l + r)

πr(l + r) = 216π

radius(r) = 9 cm

9π(l + 9) = 216π

9(l + 9) = 216

Dividing by 9 on both sides.

l + 9 = 24

Subtracting 9 on both sides.

l = 24-9

l = 15

So, the required slant height is 15 cm

Problem 5 :

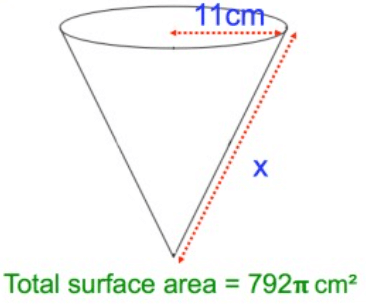
Solution :

Total surface area = πr(l + r)

πr(l + r) = 792π

radius(r) = 11 cm

11π(x + 11) = 792π

11(x + 11) = 792

Dividing by 11 on both sides.

x + 11 = 72

Subtracting 11 on both sides.

x = 72 - 11

x = 61

So, the required slant height is 61 cm

Problem 6 :

Solution :

Total surface area = πr(l + r)

πr(l + r) = 100π

radius(r) = 2 cm

2π(x + 2) = 100π

2(x + 2) = 50

Dividing by 2 on both sides.

x + 2 = 25

Subtracting 2 on both sides.

x = 25 - 2

x = 23

So, the required slant height is 23 cm.

Problem 7 :

Find the volume of the cone 

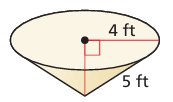
Solution :

Let r, l and h be radius, slant height and height of the cone.

l² = r² + h²

5² = 4² + h²

h² = 25 - 16

h² = 9

h = 3

Volume of cone = (1/3) πr²h

= (1/3) x 3.14 x 4² x 3

= (1/3) x 3.14 x 16 x 9

= 150.72 square feet

find the missing dimension(s) when Volume = 75.4 cm³

Problem 8 :

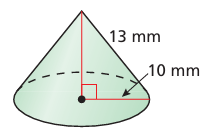
Solution :

Radius = 10 mm, slant height (l) = 13 mm

l² = r² + h²

Applying the know values, we get

13² = 10² + h²

169 - 100 = h²

h² = 69

h = √69

= 8.3 mm

Volume of cone = (1/3) πr²h 

= (1/3) x 3.14 x 10² x  8.3

= 868.73 cubic mm

Problem 9 :

A cone has a diameter of 11.5 inches and a slant height of 15.2 inches

Solution :

Radius (r) = 11.5/2 inches ==> 5.75 inches

slant height (l) = 15.2 inches

l² = r² + h²

Applying these values, we get

15.2² = 5.75² + h²

231.04 - 33.0625 = h² 

h² = 197.97

h = √197.97

= 14.07

Approximately 14.1 inches

Problem 10 :

A right cone-shaped funnel has a height of 8 centimeters and a diameter of 4.8 centimeters. Find the volume of the cone and slant height.

Solution :

Radius (r) = 4.8/2 ==> 2.4 cm

height (h) = 8 cm

l² = r² + h²

Applying these values, we get

l² = 2.4² + 8²

= 5.76 + 64

l² = 69.76

l = √69.76

l = 8.35 cm

Volume of cone = (1/3) πr²h 

= (1/3) x 3.14 x 2.4²x 8 

= 48.23 cm²

Problem 11 :

A cone has height h and a base with radius r. You want to change the cone so its volume is doubled. What is the new height if you change only the height ? What is the new radius if you change only radius ?

Solution :

Let h be the height and r be the radius.

Volume of cone = (1/3) πr²h 

When volume doubled, then 

Volume of new cone = (2/3) πr²h 

= (1/3) πr²(2h) 

So, the height should be doubled.

While changing radius :

Volume of new cone = (2/3) πr²h 

= (1/3) π(√2r)²(h)

The new radius should be √2r.

Problem 12 :

A glass in the shape of a right cone has a diameter of 3.3 inches and a slant height of 5.5 inches. Find the height of the cone.

Solution :

Radius (r) = 3.3/2 inches ==> 1.65 inches

slant height (l) = 5.5 inches

l² = r² + h²

Applying these values, we get

5.5² = 1.65² + h²

30.25 - 2.7225 = h² 

h² = 27.5275

h = √27.5275

= 5.24

So, the required height is 5.24 inches.