FIND SIDE LENGTH OF SQUARE FROM DIAGONAL

Find the length of each side.

Problem 1 :

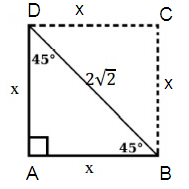
Solution :

AB = x, BD = 2√2, AD = x

Using Pythagorean theorem.

AB² + AD² = BD²

x² + x² = (2√2)²

2x² = 8

Dividing 2 on both sides.

8/2 = 2x²/2

x² = 4

x = 2 

So, the length of each side is 2.

Problem 2 :

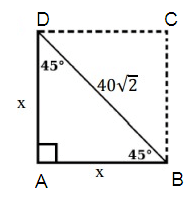
AB = x, BD = 40√2, AD = x

Using Pythagorean theorem

(BD)² = (AB)² + (AD)²

(40√2)² = x²+ x²

1600 × 2 = 2x²

3200 = 2x²

Dividing 2 on both sides.

3200/2 = 2x²/2

x² = 1600

x = 40 

So, the length of each side is 40.

Problem 3 :

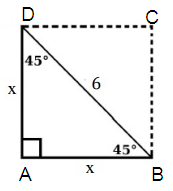
Solution :

AB = x, BD = 6, AD = x

Using Pythagorean theorem

(BD)² = (AB)² + (AD)²

6² = x²+ x²

36 = 2x²

Dividing 2 on both sides.

36/2 = 2x²/2

x² = 18

x = √(9 × 2)

x = 3√2 

So, the length of each side is 3√2.

Problem 4 :

A square has a diagonal with the length of 8√6 meters. What is the length of the sides ?

Solution :

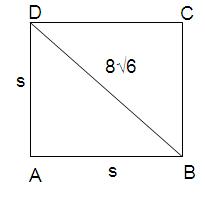
A square has a diagonal with the length of 8√6 meters. Let s be the length of the sides of the square.

Using Pythagorean theorem.

(BD)² = (AB)² + (AD)²

(8√6) ² = s² + s²

64 × 6 = 2s²

384 = 2s²

Dividing 2 on each sides.

384/2 = 2s²/2

192 = s²

s = √(64 × 3)

s = 8√3 

So, the length of each side is 8√3 .

Problem 5 :

A square has a diagonal 12√6. What is the measure of the sides of the square ?

Solution :

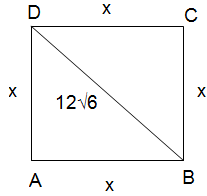
A square has a diagonal is 12√6. Let x be the sides of the square.

Using Pythagorean theorem.

(BD)² = (AB)² + (AD)²

(12√6)² = x² + x²

(12√6)² = 2x²

144 × 6 = 2x²

864 = 2x²

Dividing 2 on both sides.

864/2 = 2x²/2

432 = x²

x = √432

x = √(16 × 27)

= √(4 × 4 × 9 × 3)

= 4 × 3√3

x = 12√3

So, the measure of the sides of the square is 12√3.