FIND RECIPROCAL OF THE NUMBER

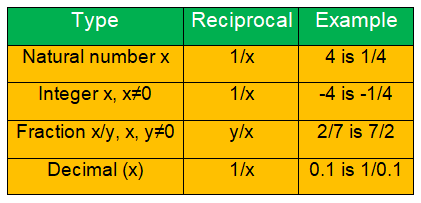
What is Reciprocal ?

In maths, reciprocal is simply defined as the inverse of a value or a number.

Find the reciprocal.

Problem 1 :

State the reciprocal of:

Solution :

a)  3/4

Reciprocal of 3/4 is 4/3

b)  2/7

Reciprocal of 2/7 is 7/2

c)  4

To consider 4 as 4/1. Reciprocal of 4/1 is 1/4.

d) -1/2

Reciprocal of -1/2 is -2/1. That is -2.

Problem 2 :

Find :

Solution :

a)  2/3 ÷ 1/6

By changing the division sign as multiplication, we can change the division sign as multiplication and write the reciprocal of second fraction.

= 2/3 x (6/1)

= 2 x (2/1)

= 4/1

= 4

b)  5/7 ÷ 1/3

= 5/7 x (3/1)

= (5 x 3) / (7 x 1)

= 15/7

Converting into mixed fraction, we get

= 2   1/7

c)  3/4  ÷ (-1/2)

= 3/4 x (-2/1)

= (-3 x 2)/(4 x 1)

= -3/2

Converting into mixed fraction, we get

= -1  1/2.

d)  4/5 ÷ 3

= 4/5 ÷ (3/1)

Convert division sign as multiplication and changing the second fraction as its reciprocal.

= 4/5 x (1/3)

= (4 x 1) / (5 x 3)

= 4/15

e)  1/4  ÷ 1  2 /3

Converting the mixed fraction 1  2/3 as improper fraction, we get

1  2/3  = 5/3

1/4  ÷ 1  2 /3 = 1/4 ÷ 5/3

= 1/4 x (3/5)

= (1 x 3) / (4 x 5)

= 3/20

f)  2   3/4  ÷  2/3

Converting 2  3/4 as improper fraction, we get 

2  3/4 = 11/4

= 11/4 ÷ 2/3

= 11/4 x (3/2)

= (11 x 3) / (4 x 2)

= 33/8

Converting into mixed fraction, we get

= 4  1/8

g)  1  1/2  ÷ (-3/4)

Converting 1  1/2 as improper fraction, we get

1  1/2 = 3/2

1  1/2  ÷ (-3/4) = 3/2  ÷ (-3/4)

= (3/2) x (-4/3)

= (-3 x 4) / (2 x 3)

= -2

h)  3  1/5  ÷ 1  1/3

Converting mixed fractions 3  1/5 as improper fraction, we get

3  1/5 = 16/5

Converting mixed fractions 1  1/3 as improper fraction, we get

1  1/3 = 4/3

3  1/5  ÷ 1  1/3 = (16/5) ÷ (4/3)

= (16/5) x (3/4)

= (16 x 3) / (5 x 4)

= (4 x 3)/5

= 12/5

= 2   2/5

Problem 3 :

A vitamin C tablet contains 1/40 of a gram of vitamin C. You take 1 1/2 tablets every day. How many grams of vitamin C do you take every day?

Solution :

Quantity of vitamin C = 1/40 grams

Daily consumption = 1 1/2 tablet ==> 3/2

Quantity of vitamin C he consumes = 1/40 of 3/2

= 1/40 x (2/3)

= 1/60 grams of vitamin C.

Problem 4 :

A science experiment calls for 3/4 cup of baking powder. You have 1/3 cup of baking powder. How much more baking powder do you need?

Solution :

Amount of baking powder needed = 3/4 cup

Amount of baking powder i have = 1/3 cup

Amount of baking powder needed = 3/4 - 1/3

= (9 - 4)/12

= 5/12 cups

Problem 5 :

Write the division problem and solve it using a model.

a. How many two-thirds are in three?

b. How many halves are in fi ve halves?

c. How many four-fi fths are in eight?

d. How many one-thirds are in seven halves?

e. How many three-fourths are in fi ve halves?

Solution :

a.

two third = 2/3

Number of two thirds in 3 = 3 ÷ (2/3)

= 3 x 3/2

= 9/2

= 4.5

Approximately 5 two thirds.

b.

Half = 1/2

Number of five halves = 5  1/2 ÷ 1/2

= 11/2 ÷ 1/2

= 11/2 x 2/1

= 11 five halves

c. How many four-fi fths are in eight?

four fifts = 4/5

number of four fifts = 8 ÷ 4/5

= 8/1 x 5/4

= 2 x 5

= 10

So, 10 four fifts are in eight.

d. How many one-thirds are in seven halves?

One thids = 1/3

Seven halves = 7  1/2

= 15/2

Number of one thirds in sevene halves = (15/2) ÷ 1/3

= 15/2 x 3/1

= (15 x 3)/(2 x 1)

= 45/2

= 22.5

Approximately 23 one thirds are in seven halves.

e. How many three-fourths are in fi ve halves?

Three fourth = 3/4

five halves = 5  1/2

= 11/2

Number of three fourths in five halves = 11/2 ÷ 3/4

= 11/2 x 4/3

= (11 x 2)/3

= 22/3

= 7.3

Approximately 7 three fourths are in five halves.