FIND RADIUS WHEN ARC LENGTH OF THE CIRCLE IS GIVEN

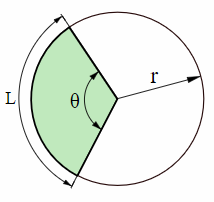
Here s is the length of arc.

Problem 1 :

s = 12π/5 ; θ = π/2 ; r = ?

Solution :

Arc length of the circle s = rθ

12π/5 = r × π/2

12π/5 × 2/π = r

24/5 = r

So, the radius r is 24/5 .

Problem 2 :

s = 50π/3 in ; θ = 5π/6 ; r = ?

Solution :

Arc length of the circle s = rθ

50π/3 = r × 5π/6

50π/3 × 6/5π = r

20 = r

So, the radius r is 20 .

Problem 3 :

s = 7ft ; θ = 3π/4 ; r = ?

Solution :

Arc length of the circle s = rθ

7 = r × 3π/4

7 × 4/3π = r

28/3π = r

28/(3 × 22/7) = r

196/66 = r

So, the radius r is 196/66 ft .

Problem 4 :

s = 20 cm ; θ = 2π/3 ; r = ?

Solution :

Arc length of the circle s = rθ

20 = r × 2π/3

20 × 3/2π = r

60/2π = r

30/(22/7) = r

So, the radius r is 105/22 cm .

Problem 5 :

s = 12 in ; θ = 5 ; r = ?

Solution :

Arc length of the circle s = rθ

12 = r ×5

12/5 = r

So, the radius r is 12/5 in.

Problem 6 :

s = 7 in ; θ = 3 ; r = ?

Solution :

Arc length of the circle s = rθ

7 = r × 3

7/3 = r

So, the radius r is 7/3 in.

Problem 7 :

s = 15 m ; θ = 270 ; r = ?

Solution :

Arc length of the circle s = rθ

15 = r × 270

15/270 = r

1/18 = r

So, the radius r is 1/18 m.

Problem 8 :

s = 8 yd ; θ = 225 ; r = ?

Solution :

Arc length of the circle s = rθ

8 = r × 225

8/225 = r

28.125 = r

So, the radius r is 28.125 yd.