FIND RADIUS OF CYLINDER OF  GIVEN SURFACE AREA

Work out the radius of each cylinder below

Problem 1 :

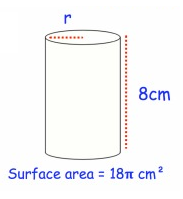
Solution :

By observing the figure,

Radius r = ?

Height h = 8 cm

Surface area A = 18π cm²

Surface area A= 2πr(h + r)

18π = 2πr(8 + r)

Divide each side by 2π.

18π/2π = (2πr(8 + r))/2π

9 = r(8 + r)

9 = 8r + r²

 r² + 8r – 9 = 0

(r + 9)(r - 1) = 0

r = 1 cm

Problem 2 :

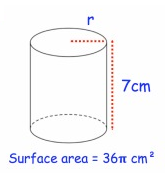
Solution :

By observing the figure,

Radius r = ?

Height h = 7 cm

Surface area A = 36π cm²

Surface area A= 2πr(h + r)

36π = 2πr(7 + r)

Divide each side by 2π.

36π/2π = (2πr(7 + r))/2π

18 = r(7 + r)

18 = 7r + r²

 r² + 7r – 18 = 0

r = 2 cm

Problem 3 :

The radius and height of a cylinder are 5 : 7 and volume is 550 cm³. Find the total surface area.

Solution :

Radius = 5x and height = 7x

Volume of cylinder = 550 cm³

πr²h = 550

Radius = 5(1) ==> 5

height = 7(1) ==> 7

Total surface area of cylinder = 2πr(h + r)

= 2π . 5(7 + 5)

= 10π (12)

= 120π cm²

Problem 4 :

The circumference of the base of a right circular cylinder is 220 cm. If the height of the cylinder is is 2 m, find the total  surface area of cylinder.

Solution :

Circumference of the base of cylinder = 220 cm

2πr = 220

2. (22/7) . r = 220

r = 220 . (7/22) . (1/2)

r = 35

h = 2 m

Curved surface area of cylinder = 2πr(h + r)

Problem 5 :

A roller of diameter 70 cm and the length 2 m is rolling on the ground. What is the area by the roller in 50 revolutions ?

Solution :

Radius of the roller = 70 cm

height of the roller = 2 m ==>  200 cm

Area covered in revolution = 2πrh

= 2 . (22/7) . 70 . 200

= 88000 cm²

= 8.8 m²

Area covered in 50 revolution = 8.8 (50)

= 440 m²

Problem 6 :

A ganza is a percussion instrument used in samba music.

a. Find the surface area of each of the two labeled ganzas.

b. The weight of the smaller ganza is 1.1 pounds. Assume that the surface area is proportional to the weight. What is the weight of the larger ganza?

Solution :

Total surface area of small ganzas = 2πr(h + r)

radius = 3.5/2 ==> 1.75 cm, height = 10 cm

= 2 x π x 1.75 (10 + 1.75)

= 3.5 x π (11.75)

= 41.125 π cm²

Total surface area of large ganzas = 2πr(h + r)

radius = 5.5/2 ==> 2.75 cm, height = 24.5 cm

= 2 x π x 2.75 (24.5 + 2.75)

= 5.5 x π (27.25)

= 149.875 π cm²

Weight of smaller gazna = 1.1 pounds

Weight of larger gazna = x pounds

41.125 π/149.875 π = 1.1/x

0.2743 = 1.1/x

x = 1.1/0.2743

x = 4.010

Approximately 4 pounds.

Problem 7 :

The cut wedge represents one-eighth of the cheese.

a. Find the surface area of the cheese before it is cut.

b. Find the surface area of the remaining cheese after the wedge is removed. Did the surface area increase, decrease, or remain the same?

Solution :

a) 

Surface area = 2πr(h + r)

r = 3 inches and height = 1 inch

= 2 x 3.14 x 3 (3 + 1)

= 6.28 x 3(4)

= 75.36 square inch

b) 1/8 of the widge is removed.

Surface area of the remaining part = 7/8 of surface area

= 7/8 of 75.36

= 7(75.36)/8

= 65.94 square inches

So, the removed widge is lesser than the original amount of cheese.

Problem 8 :

The lateral surface area of a cylinder is 184 square centimeters. The radius is 9 centimeters. What is the surface area of the cylinder? Explain how you found your answer.

Solution :

Lateral surface area of cylinder = 184 square cm

2πrh = 184 square cm

radius = 9 cm

Surface area = 2πr(h + r)

= 2πrh + 2πr²

= 184 + 2 x 3.14 x 9²

= 184 + 508.68

= 692.68 square cm

Problem 9 :

The lateral surface area of a right circular cylinder of height 7 cm is 44 cm². Find the diameter of the base of the cylinder ?

Solution :

Lateral surface area of cylinder = 44 cm²

2πrh = 44

h = 7 cm

2 x 3.14 x r x 7 = 44

43.96 x r = 44

r = 44/43.96

r = 1.00

diameter = 2r ==> 2(1)

= 2 cm

So, the required diameter of the cylinder is 2 cm.