FIND RADIUS OF CONE WHEN GIVEN SURFACE AREA

Find length of radius of the following cones given below.

Problem 1 :

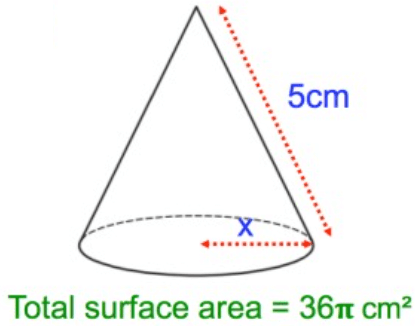
Solution :

Total surface area = πr(l + r)

πr(l + r) = 36π

radius(r) = x and slant height (l) = 5 cm

xπ(5 + x) = 36π

5x + x² = 36

x² + 5x - 36 = 0

(x + 9) (x - 4) = 0

x = -9 and x = 4

So, the required radius is 4 cm.

Problem 2 :

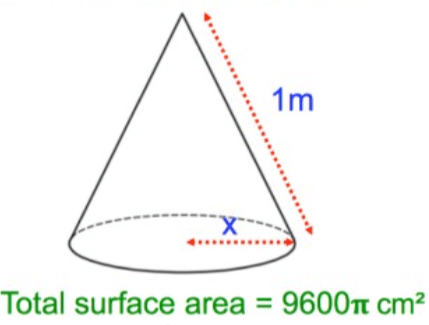
Solution :

Total surface area = πr(l + r)

πr(l + r) = 9600π

radius(r) = x and slant height (l) = 1 m = 100 cm

xπ(100 + x) = 9600π

100x + x² = 9600

x² + 100x  - 9600 = 0

(x + 160)(x - 60) = 0

x = -160 and x = 60

So, the radius is 60 cm.

Problem 3 :

The cylinder and cone has the same surface area. Express L in terms of x.

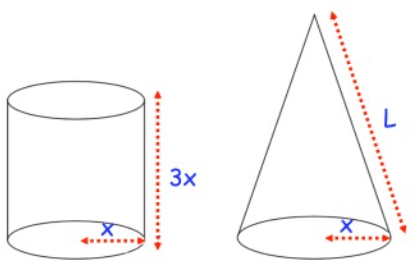
Solution :

Surface area of cylinder = 2πr(h + r)

Surface area of cone = πr(l + r)

height of cylinder = 3x and slant height of cone = l

2πx(3x + x) = πx(l + x)

2x(4x) = x(l + x)

8x² = lx + x²

Subtracting x² on both sides.

7x² = lx

l = 7x

Problem 4 :

A cone and cylinder are joined to make a solid

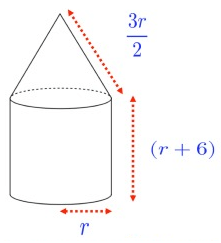
Find the total surface area of the solid.

Solution :

Total surface area of the figure given above = 

lateral surface area of cylinder + lateral surface area of cone

= 2πrh + πrl

= πr(2h + l)

= πr(2(r+6) + (3r/2))

= πr(2r + 12 + (3r/2))

= πr((4r + 24 + 3r)/2)

= πr((7r + 24)/2)

Problem 5 :

You are making a skylight that has 12 triangular pieces of glass and a slant height of 3 feet. Each triangular piece has a base of 1 foot

Solution :

Area of triangular piece = (1/2) x base x height

base = 0.5 feet, slant height = 3 feet

l² = r² + h²

3² = 0.5² + h²

h² = 9 - 0.25

h² = 8.75

h = √8.75

h = 2.95 feet

Area of triangular pieces cone = 12 x (1/2) x 0.5 x 2.95

= 6 x 0.5 x 2.95

= 8.85 square feet

Problem 6 :

A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 6 cm and its height is 4 cm. find the cost of painting the toy at the rate of dollar, 5 per 1000 cm².

Solution :

Diameter = 6 cm, radius = 3 cm and height = 4 cm

l² = r² + h²

l² = 3² + 4²

l² = 9 + 16

l² = 25

l = 5 cm

area to be painted = Surface area of cone + surface area of hemisphere

= πrl + 2πr²

= πr(l + 2r)

= 3.14(3)(5 + 2(3))

= 9.42(5 + 6)

= 9.42(11)

= 103.62 square cm

$5 per 1000 cm²

1 cm² = 5/1000

103.62 square cm = (1/200) x 103.62

= $0.51 

So, the required cost is $0.51.

Problem 7 :

The cone and cube below have the same surface areas. Work out the side length of the cube.

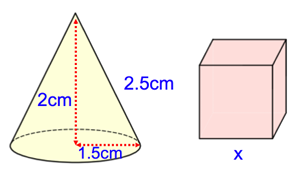
Solution :

Surface area of cone = surface area of cube

πrl = 4a²

3.14 x 1.5 x 2.5 = 4x²

x² = (3.14 x 1.5 x 2.5)/4

x² = 2.943

x = 1.71

So, the side length of the cube is 1.71 cm.

Problem 8 :

The diagram shows a solid shape. The shape is a cone on top of a cylinder. Work out the surface area of the shape. Give your answer correct to 2 significant

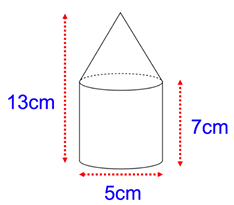
Solution :

Radius = 2.5 cm, height of cylinder = 7 cm, height of cone = 13 - 7 ==> 6 cm

Slant height of cone l² = r² + h² 

l² = 2.5² + 6²

l² = 6.25 + 36

l² = 42.25

l = 6.5 cm

Surface area of the shape = surface area of cylinder + surface area of cone

= 2πrh + πrl

= πr(2h + l)

= 3.14 x 2.5 [2(7) + 6.5]

= 7.85[14 + 6.5]

= 7.85 (20.5)

= 160.92 cm²

Problem 9 :

A cone has a radius of 9 cm. The surface area of the cone is 450 π cm² Work out the volume of the cone. Give your answer in terms of π

Solution :

Radius = 9 cm

Surface area = 450 π cm²

Volume of cone = 1/3 πr² h

πrl = 450 π

9 x l = 450

l = 450/9

l = 50

l² = r² + h² 

50² = 9² + h² 

2500 - 81 = h² 

h² = 2419

h = 49.18

Applying these values, we get

= 1/3 x 3.14 x 9² x 49.18

= 1.04 x 81 x 49.18

= 4142.92 cm³

Problem 10 :

The diagram shows a solid shape. The shape is a cone on top of a hemisphere. Work out the surface area of the shape. Give your answer correct to 2 significant figure.

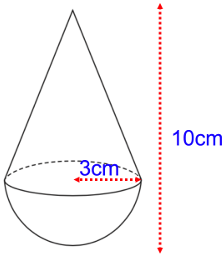
Solution :

Surface area of the figure = Surface area of hemisphere + surface area of cone

= (2/3) πr³ + πrl

Radius of hemisphere = radius of cone = 3 cm, height of cone = 10 - 3 ==> 7 cm

l² = r² + h² 

l² = 3² + 7² 

= 9 + 49

l² = 58

l = √58

l = 7.61

= πr[(2/3)r² + l]

= π(3)[(2/3)3² + 7.61]

= 3π18+7.61]

= 76.83π cm²