FIND QUARTILES FROM BOX AND WHISKER PLOT

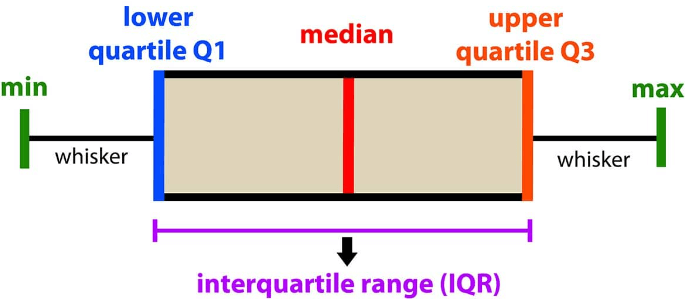
A quartile divides data into three points

• a lower quartile
• median
• upper quartile

to form four groups of the dataset.

What is lower quartile ?

The lower quartile, or first quartile, is denoted as Q₁. 

How to calculate lower quartile or Q₁?

It can be calculated in two different ways.

Q₁ = Median value of lower half of the data.

Using the formula (n + 1)/4 the value.

What is upper quartile ?

The upper quartile, or third quartile, is denoted as Q₃. 

How to calculate upper quartile or Q₃?

It can be calculated in two different ways.

Q₃ = Median value of upper half of the data.

Using the formula 3(n + 1)/4 the value.

What is median ?

The median is denoted as Q₂. 

Problem 1 :

According to the box-and-whisker plot, what was the lower quartile weight of Frank’s classmates?

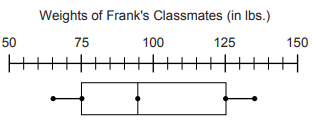
(a) 65       (b) 75     (c) 95     (d) 125

Solution :

From the box plot 95 is the median. 

Lower quartile (Q₁) = 75

Problem 2 :

According to the box-and-whisker plot, what was the upper quartile of gallons of paint sold at John’s Hardware Store in a month?

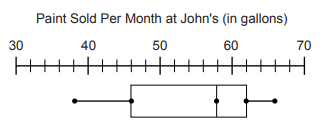
 (a) 58      (b) 60   (c) 61     (d) 62

Solution :

From the box plot 58 is the median. 

Upper quartile (Q₃) = 62 gallons

Problem 3 :

According to the box-and-whisker plot, what was the median weight of a pumpkin at the annual pumpkin festival?

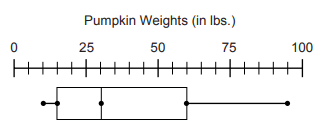
(a) 30    (b) 37.5     (c) 52.5     (d) 60

Solution :

From the box plot, the median Q₂ = 30 lbs.

Problem 4 :

According to the box-and-whisker plot, what was the maximum number of hot dogs eaten in the hot dog eating contest?

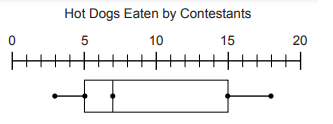
 (a) 3      (b) 7     (c) 15      (d) 18

Solution :

Maximum value = 18

Problem 5 :

What is the median of the data set represented by the box-and-whisker plot?

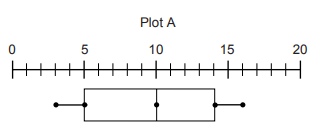
(a) 5       (b) 10       (c) 15        (d) 16

Solution :

Median = 10

Problem 6 :

According to the box-and-whisker plot, what was the lower quartile of meals served in a day at Susan’s Diner?

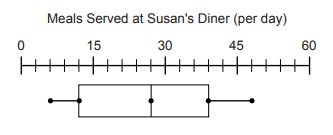
(a) 3       (b) 6        (c) 12         (d) 14

Solution :

Lower quartile (Q₁) = 12

Problem 7 :

For questions 1 – 5, refer to the box & whisker graph below which shows the test results of a math class.

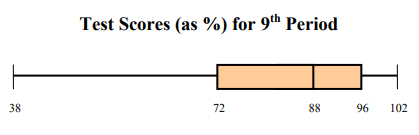
1) What was the high score on the test? 

2) What percent of the class scored above a 72? 

3) What was the median score on the test? 

4) What percent of the class scored between 88 & 96?

5) Do you think that this test was too hard for the students? Explain.

Solution :

1) What was the high score on the test? 

102 is the highest score of the test.

2) What percent of the class scored above a 72? 

The box plot shows 100% of the data. 

38 - 72 = 25% of the data

72 to 88 = 25% of the data, 88 to 96 = 25% of data, 96 to 102 = 25% of the data

Percentage of students scored above 72 :

= 25% + 25% + 25%

= 75%

3) What was the median score on the test? 

Median score = 88

4) What percent of the class scored between 88 & 96?

25% of the class has scored between 88 to 96.

5) Do you think that this test was too hard for the students? Explain.

No, 50% of the students has scored between 88 to the maximum score 102. So, the test was not too hard.

Problem 8 :

Refer to the box & whisker graphs below that compare homework time per night with TV time per night for the same group of sophomores.

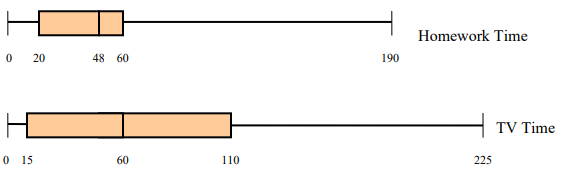
1) What percent of the sophomores watch TV for at least 15 minutes per night?

2) What is the 3^rd quartile for the TV time data?

Solution :

1) 25% of the sophomores are watching TV for at least 15 minute per night.

2) 3^rd quartile (Q₃) = 110

Problem 9 :

Refer to the box & whisker graphs below that show the average monthly high temperatures for Milwaukee, Wisconsin & Honolulu, Hawaii.

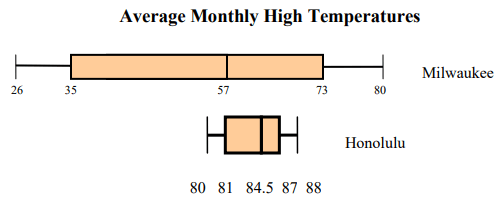
Complete the table using the box and whisker plots for Honolulu and Milwaukee.

Solution :