FIND POINTS OF INTERSECTION OF CIRCLE AND LINE

A straight line and circle can have two, one or no points of intersection:

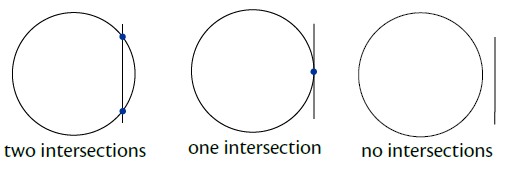
If a line and a circle only touch at one point, then the line is a tangent to the circle at that point.

To find out how many times a line and circle meet, we can use substitution.

Problem 1 :

Find the points where the line with equation y = 3x intersects the circle with equation x² + y² = 20 .

Solution :

y = 3x -----(1)

x² + y² = 20 -----(2)

Applying the value of y in (2), we get

x² + (3x)² = 20

x² + 9x²= 20

10x² = 20

x² = 2

x =  ±√2

When x = √2, y = 3√2

When x = -√2, y = -3√2

So, the points of intersections are (√2, 3√2) and (-√2, -3√2).

Problem 2 :

Find the points where the line with equation y = 2x + 6 and circle with equation x² + y² + 2x + 2 y − 8 = 0 intersect.

Solution :

y = 2x + 6 ----(1)

x² + y² + 2x + 2 y − 8 = 0  ----(2)

Applying the value of y in (2), we get

x² + (2x + 6)² + 2x + 2(2x + 6) − 8 = 0

x² + 4x² + 24x + 36 + 2x + 4x + 12 - 8 = 0

x² + 4x² + 30x + 40 = 0

5x² + 30x + 40 = 0

x² + 6x + 8 = 0

(x + 2) (x + 4) = 0

x = -2 and x = -4

When x = -2, y = 2(-2) + 6 ==> 2

When x = -4, y = 2(-4) + 6 ==> -2

So, the points of intersections are (-2, 2) and (-4, -2).

Problem 3 :

Find the points of intersection of the line y = 2x + 8 and the circle with equation x² + y² + 4x + 2y – 20 = 0.

Solution :

y = 2x + 8 ----(1)

x² + y² + 4x + 2y − 20 = 0  ----(2)

Applying the value of y in (2), we get

x² + (2x + 8)² + 4x + 2(2x + 8) − 20 = 0

x² + 4x² + 32x + 64 + 4x + 4x + 16 - 20 = 0

x² + 4x² + 40x + 80 - 20 = 0

5x² + 40x + 60 = 0

x² + 8x + 12 = 0

(x + 6) (x + 2) = 0

x = -6 and x = -2

When x = -6, y = 2(-6) + 8 ==> -4

When x = -2, y = 2(-2) + 8 ==> 4

So, the points of intersections are (-6, -4) and (-2, 4).

Problem 4 :

Find the points of intersection of the circle

x² + y² – 2x – 4y + 1 = 0

and the line

x + y = 1.

Solution :

x² + y² – 2x – 4y + 1 = 0 ---(1)

x + y = 1 ----(2)

y = 1 - x

x² + (1 - x)² - 2x - 4(1 - x) + 1 = 0

x² + 1 + x² - 2x - 2x - 4 + 4x + 1 = 0

2x² - 4x + 4x - 2 = 0

2x² - 2 = 0

(x² - 1) = 0

(x + 1)(x - 1) = 0

x = 1 and x = -1

When x = 1, y = 1 - 1 ==> 0

When x = -1, y = 1 - (-1) ==> 2

So, the points of intersections are (1, 0) and (-1, 2).