FIND MISSING SIDE WHEN GIVEN PERIMETER

Find the unknown side length of the triangle given the perimeter P. Then classify the triangle by its side lengths.

Problem 1 :

If the perimeter of the given triangle is 49 inches, find the missing side.

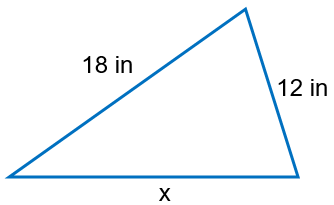
Solution :

Perimeter of a triangle = Sum of the length of all its sides.

Let s₁, s₂ and s₃ be the sum of the length of sides respectively.

The perimeter of a triangle = 49 in.

Let s₁ = 18,  s₂ = 12 and s₃ = x

49 = s₁ + s₂ + s₃

18 + 12 + x = 49

 30 + x = 49

 x = 49 - 30

x = 19 in

Every side is having different measures, so it is a scalene triangle.

Problem 2 :

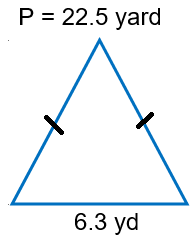
Solution :

The perimeter of a triangle = The sum of the length of sides respectively.

Let s₁, s₂ and s₃ be the sum of the length of all its sides.

The perimeter of a triangle = 22.5 yd.

Let s₁ = 6.3,  s₂ = x and s₃ = x

22.5 = s₁ + s₂ + s₃

 6.3 + x + x = 22.5

6.3 + 2x = 22.5

 2x = 22.5 – 6.3

2x = 16.2

x = 16.2/2

x = 8.1 yd

Two sides are equal. So it is isosceles triangle.

Problem 3 :

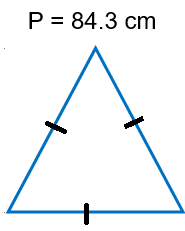
Solution :

The perimeter of a triangle = Sum of the length of sides 

Let s₁, s₂ and s₃ be the sum of the length of all its sides respectively.

The perimeter of a triangle = 84.3 cm.

Let s₁ = x, s₂ = x and s₃ = x

84.3 = s₁ + s₂ + s₃

x + x + x = 84.3

3x = 84.3

x = 84.3/3

x = 28.1 cm

Every side is equal, so it is equilateral triangle.

Problem 4 :

The perimeter of a triangle is 29 millimeters. The length of the first side is twice the length of the second side. The length of the third side is 5 more than the length of the second side. Find the side lengths of the triangle. Then classify the triangle by its side lengths.

Solution :

The perimeter of a triangle = Sum of the length of all its sides.

Length of the sides be s_1, s₂ and s₃ respectively.

s₁ = 2s₂

The length of the third side is 5 more than the length of the second side.

s₃ = s₂ + 5

s₁ + s₂ + s₃ = 29

2s₂ + s₂ + s₂ + 5 = 29

4s₂ + 5 = 29

4x = 29 – 5

4x = 24

x = 24/4

x = 6 

Problem 5 :

The perimeter of a triangular window is 141 inches. The ratio of the side lengths of the window is 11 : 18 :18. Draw and label a diagram of the window. What are the side lengths of the window? Classify the window by its side lengths.

Solution :

The perimeter of a triangle = The sum of the length of all its sides.

Let s₁ , s₂  and s₃ be the sum of the length of all its sides.

The perimeter of a triangular window = 141 inches.

The ratio of the side lengths of the window = 11 : 18 : 18

s₁ + s₂ + s₃ = 141

Let s₁ = 11 x, s₂ = 18x and s₃ = 18x                   

11x +18x +18x =141

47x = 141

x = 141/47

x = 3

11(3) = 33 ; 18(3) = 54 ; 18(3) = 54

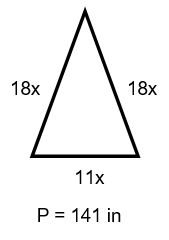
Therefore the side lengths of the window are 33 in, 54in, 54 in.

Two equal sides and two equal angles. So it is isosceles triangle.

Problem 6 :

The ratio of the angle measures of a triangle is 7 : 16 : 22. Find the angle measures. Then classify the triangle by its angle measures.

Solution :

The ratio of the angle measures of a triangle are 7 : 16 : 22.

The angle of a triangle = 180°

7x +16x +22x =180°

45x = 180°

x = 180°/45

x = 4

The angle measures are,

7(4) = 28° ; 16(4) = 64° ; 22(4) = 88°

Problem 7 :

The ratio of the side lengths of a triangle is 7 : 24 : 25. The perimeter of the triangle is 392 inches.

a) Find the side lengths. Then classify the triangle by its side lengths.

b) is the triangle a right triangle ? How do you know?

Solution :

a) The ratio of the side lengths of a triangle are in the ratio

7 : 24 : 25

The perimeter of the triangle = 392 inches

7x + 24x +25x = 392

56x = 392

x = 392/56

x = 7

Therefore the side lengths are,

7(7) = 49 ; 24(7) = 168 ; 25(7) = 175

= 49 in ;168 in; 175 in

Every side is having different measures, so it is scalene triangle.

b) yes it is right triangle. It is used Pythagorean theorem.

49² + 168² = 175²

2401 + 28224 = 30625

Since it satisfies Pythagorean theorem, it is right triangle.