FIND MISSING MEASURES WHEN GIVEN SURFACE AREA

Problem 1 :

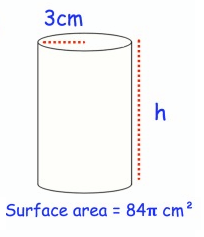
Solution :

Radius r = 3 cm

Surface area = 84π cm²

Surface area of cylinder = 2πrh

84π = (2) (3) π h

84 = 6h

h = 84/6

h = 14 cm

Height of cylinder is 14 cm.

Problem 2 :

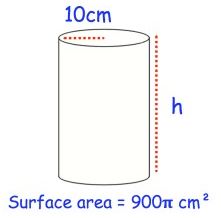
Solution :

Radius r = 10 cm

Surface area = 900π cm²

Surface area of cylinder = 2πrh

900π = (2) (10) π h

900 = 20h

h = 900/20

h = 45 cm

Height of cylinder is 45 cm.

Problem 3 :

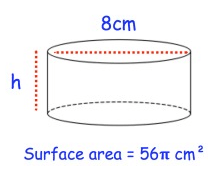
Solution :

Radius r = 8 cm

Surface area = 56π cm²

Surface area of cylinder = 2πrh

56π = (2) (8) π h

56 = 16h

h = 56/16

h = 3.5 cm

Height of cylinder is 3.5 cm.

Work out the radius of each cylinder below

Problem 4 :

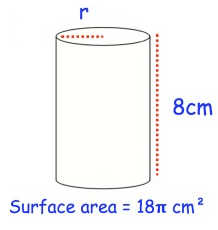
Solution :

Height h = 8 cm

Surface area = 18π cm²

Surface area of cylinder = 2πrh

18π = (2) (8) π r

18 = 16r

r = 18/16

r = 1.125 cm

Radius of cylinder is 1.125 cm.

Problem 5 :

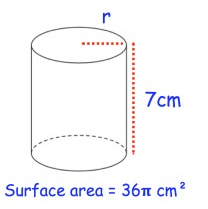
Solution :

Height h = 7 cm

Surface area = 36π cm²

Surface area of cylinder = 2πrh

36π = (2) (7) π r

36 = 14r

r = 36/14

r = 2.571 cm

Radius of cylinder is 2.571 cm.

Problem 6 :

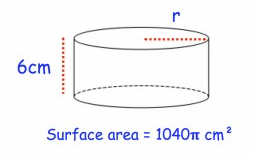
Solution :

Height h = 6 cm

Surface area = 1040π cm²

Surface area of cylinder = 2πrh

1040π = (2) (6) π r

1040 = 12r

r = 1040/12

r = 86.7 cm

Radius of cylinder is 86.7 cm.

Problem 7 :

The surface area of a square pyramid is 84 square inches. The side length of the base is 6 inches. What is the value of x

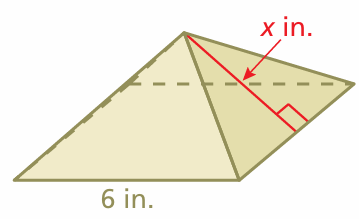
Solution :

Surface area of pyramid = 84 square inches

Area of square base + 4(area of triangle faces) = 84

6² + 4 ⋅ 1/2 ⋅ base ⋅ height = 84

36 + 2⋅6⋅x = 84

36 + 12x = 84

12x = 84 - 36

12x = 48

x = 48/12

x = 4 inch

So, the required slant height of the prism is 4 inch.

Problem 8 :

The Great Pyramid of Giza is a square pyramid. A gift shop sells miniature models of this pyramid. Find the surface area of the model shown at the left

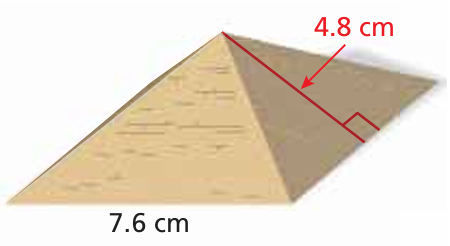
Solution :

Side length of square base = 7.6 cm

Surface area = Area of square base + 4(area of triangle faces)

= (7.6)² + 4 ⋅ 1/2 ⋅ base ⋅ height

= 57.76 + 2 ⋅ (7.6) ⋅ (4.8)

= 57.76 + 72.96

= 130.72 square cm

So, the required surface area of square pyramid is 130.72 square cm.

Problem 9 :

A tetrahedron is a triangular pyramid whose four faces are identical equilateral triangles. The total lateral surface area is 93 square centimeters. Find the surface area of the tetrahedron.

Solution :

total surface area of pyramid inlcudes area of 4 faces.All are identitical equilateral triangles.

The lateral surface area consists of the three side faces. Since all four faces are identical, we can find the area of one face by dividing the total lateral surface area by

area of one face = 93/3

= 31 square cm

Total surface area = 4(31)

= 123 square cm

Problem 9 :

The entrance to the Louvre Museum in Paris, France, is a square pyramid. The side length of the base is 116 feet, and the height of one of the triangular faces is 91.7 feet. Find the surface area of the four triangular faces of the entrance to the Louvre Museum.

Solution :

Side length of the base = 116 feet

height of the triangular face = 91.7 feet

Surface area of the prism = area of base of square + 4 x area of triangular faces

= (116)² + 4 (1/2) x 116 x 91.7

= 13456 + 2 x 116 x 91.7

= 13456 + 21274.4

= 34730.4 square feet

Problem 10 :

A hanging light cover made of glass is shaped like a square pyramid. The cover does not have a bottom. One square foot of the glass weighs 2.45 pounds. The chain can support 35 pounds. Will the chain support the light cover? Explain.

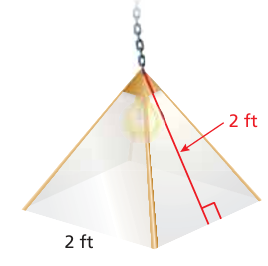
Solution :

Side length of the base = 2 ft

Slant height of prism or height of triangular face = 2 ft

Surface area of the prism = area of base of square + 4 x area of triangular faces

= 2² + 4 (1/2) x 2 x 2

= 4 + 0.5

= 4.5 square feet

Problem 11 :

In the diagram of the base of the hexagonal pyramid, all the triangles are the same. Find the surface area of the hexagonal pyramid.

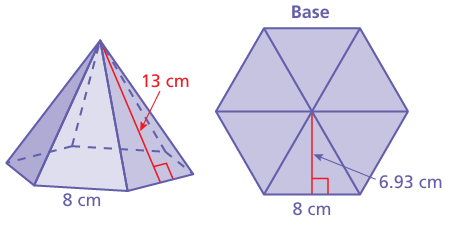
Solution :

Surface area of the shape = area of hexagonal base + 6 x arae of triangular faces

Finding area of hexagonal base :

= 1/2 x apothem x perimeter

= (1/2) x 6.93 x 8

= 4 x 6.93

= 27.72 cm²

Suraface area = 27.72 + 6 x (1/2) x 8 x 13

= 27.72 + 3 x 8 x 13

= 27.72 + 24 x 13

= 27.72 + 312

= 339.72 cm²