FIND MISSING LENGTH OF SIMILAR TRIANGLES

Find the missing length. The triangles in each pair are similar.

Problem 1 :

Solution:

Because the above triangle ∆ PQR and ∆ EDC are similar, the ratios of the corresponding sides will be equal.

Problem 2 :

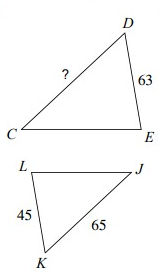
Solution:

Because the above triangle ∆ DCE and ∆ KJL are similar, the ratios of the corresponding sides will be equal.

Let x = DC

Problem 3 :

Solution:

Because the above triangle ∆ ABC and ∆ AKL are similar, the ratios of the corresponding sides will be equal.

Problem 4 :

Solution:

Because the above triangle ∆ HJG and ∆ KJL are similar, the ratios of the corresponding sides will be equal.

Solve for x. The triangles in each pair are similar.

Problem 5 :

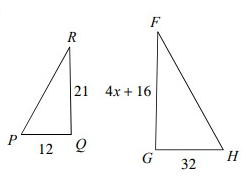
Solution:

Because the above triangle ∆ RQP and ∆ FGH are similar, the ratios of the corresponding sides will be equal.

Problem 6 :

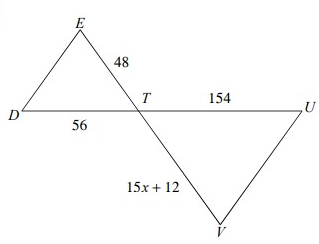
Solution:

Because the above triangle ∆ EDT and ∆ VTU are similar, the ratios of the corresponding sides will be equal.

Problem 7 :

In the following figure, JKLM ∼ EFGH

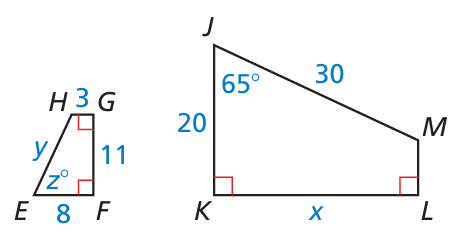
a) Find the scale factor of JKLM to EFGH.

b) Find the scale factor of EFGH to JKLM.

c) Find the values of x, y, and z.

d)  Find the perimeter of each polygon.

e) Find the ratio of the perimeters of JKLM to EFGH.

f)  Find the area of each polygon.

g) Find the ratio of the areas of JKLM to EFGH.

Solution :

a) Since the following figures are similar, corresponding sides will be in the same ratio and corresponding angles will be equal.

z = 65

Corresponding sides are :

• ML and HG
• JK and EF
• JM and EH
• KL and GF

Ratio between the corresponding sides is = 20 : 8

= 5 : 2

So, the required scale factor between JKLM to EFGH is 5 : 2.

b) the required scale factor between EFGH and JKLM to is 2 : 5.

c) HG/ML = EF/JK = EH/JM = GF/KL

3/ML = 8/20 = y/30 = 11/x

8/20 = 11/x

8x = 11(20)

x = 220/8

x = 27.5

d)  Perimeter of the EFGH = 8 + 11 + 3 + y

= 22 + 12

= 34

Perimeter of JKLM = 20 + x + ML + 30

= 20 + 27.5 + 7.5 + 30

= 85

e) Ratio of the perimeters of JKLM to EFGH = 85 : 34

f)  Area of trapezium EFGH = (1/2) x height x sum of parallel sides

= (1/2) x 11 (8 + 3)

= 1/2 x 11 x 11

= 121/2

= 60.5 square units

Area of  trapezium JKLM = (1/2) x 27.5 (20 + 7.5)

= (1/2) x 27.5 x 27.5

= 378.125 square units

g) Ratio of the areas of JKLM to EFGH = 378.125 : 60.5

= 6.25 : 1

= 625 : 100

= 25 : 4

So, the ratio between the areas is 25 : 4.

Problem 8 :

Rectangle A is similar to rectangle B. Rectangle A has side lengths of 6 and 12. Rectangle B has a side length of 18. What are the possible values for the length of the other side of rectangle B? Select all that apply.

a) 6     b)  9    c)  24    d) 36

Solution :

Let x be the missing length of rectangle B.

6 : 18 = 12 : x

6/18 = 12/x

6x = 12(18)

x = 12(18)/6

x = 12(3)

= 36

So, option d is correct.