FIND MISSING COORDINATE WHEN SLOPE IS GIVEN

Find the value of x and y so that the line through the pair of points has the given slope.

Problem 1 :

(x, 3) and (5, 9) and slope (m) = 2

Solution :

Let (x₁, y₁) ==> (x, 3) and (x₂, y₂) ==> (5, 9)

m = (9 - 3) / (5 - x)

By applying the value of m, we get

2 = 6/(5 - x)

Doing cross multiplication, we get

5 - x = 12

Subtracting 5 on both sides, we get

-x = 12 - 5

-x = 7

x = -7

So, the value of x is -7.

Problem 2 :

(-2, 3) and (4, y) and slope (m) = -3

Solution :

Let (x₁, y₁) ==> (-2, 3) and (x₂, y₂) ==> (4, y)

m = (y - 3) / (4 - (-2))

m = (y - 3) / 6

By applying the value of m, we get

-3 = (y - 3) / 6

Doing cross multiplication, we get

y - 3 = -3(6)

y - 3 = -18

Add 3 on both sides, we get

y = -18 + 3

y = -15

So, the value of y is -15.

Problem 3 :

(-3, -5) and (4, y) and slope (m) = 3

Solution :

Let (x₁, y₁) ==> (-3, -5) and (x₂, y₂) ==> (4, y)

m = (y - (-5)) / (4 - (-3))

m = (y + 5) / 7

By applying the value of m, we get

3 = (y + 5) / 7

Doing cross multiplication, we get

y + 5 = 3(7)

y + 5 = 21

Subtract 5 on both sides, we get

y = 21 - 5

y = 16

So, the value of y is 16.

Problem 4 :

(-8, -2) and (x, 2) and slope (m) = 1/2

Solution :

Let (x₁, y₁) ==> (-8, -2) and (x₂, y₂) ==> (x, 2)

m = (2 - (-2)) / (x - (-8))

m = 4 / (x + 8)

By applying the value of m, we get

1/2 = 4 / (x + 8)

Doing cross multiplication, we get

x + 8 = 4(2)

x + 8 = 8

Subtracting 8 on both sides. We get

x = 8 - 8

x = 0

So, the value of x is 0.

Problem 5 :

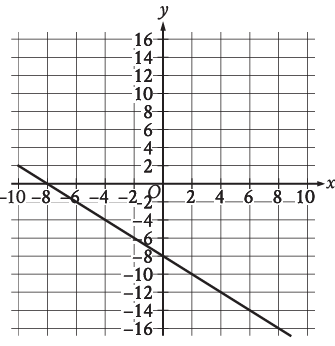
What is an equation of the graph shown?

a) y = −2x − 8     b) y = x - 8       c) y = − x − 8      d) y = 2 x − 8

Solution :

Tracing two points on the line is (-8, 0) and (0, -8).

Slope = (y₂ - y₁) / (x₂ - x₁)

= (-8 - 0) / (0 - (-8))

= -8/(0 + 8)

= -8/8

= -1

y-intercept = -8

Equation of the line :

y = mx + b

y = -1x + (-8)

y = -1x - 8

Problem 6 :

f(x) = 2x + 3

For the given function f, the graph of y = f(x) in the xy-plane is parallel to line j. What is the slope of line j ?

Solution :

f(x) = 2x + 3

By comparing the given equation with y = mx + b

Slope of the line f(x) = 2

When two lines are parallel, their slopes will be equal. So, slope of the require line j is also 2.

Problem 7 :

Line l goes through points P and Q, whose coordinates are (0, 1) and (b, 0), respectively. For which of the following values of b is the slope of line l greater than −1/2 ?

a) 1/2       b)  1       c) 3/2      d)  5/3      e)  5/2

Solution :

(0, 1) and (b, 0)

Slope of the line j = (y₂ - y₁) / (x₂ - x₁)

-1/2 = (0 - 1) / (b - 0)

-1/2 < -1/b

1/2 > 1/b

b > 2

So, option e is correct.

Problem 8 :

The function h is defined by h(x) = 4x + 28. The graph of y = h(x) in the xy-plane has an x-intercept at (a, 0) and a y-intercept at (0, b), where a and b are constants. What is the value of a + b ?

a) 21       b)  28       c) 32      d)  35

Solution :

h(x) = 4x + 28

a + b = -7 + 28

= 21

So, option a is correct.

Problem 9 :

Lien l is defined by 3y + 12x = 5. The line n is perpendicular to the line l in the xy-plane. What is the slope of line n ?

Solution :

3y + 12x = 5

3y = -12x + 5

y = (-12/3) x + 5/3

y = -4x + (5/3)

Slope of the given line is -4

When two lines are perpendicular, their product of the slopes will be equal to -1.

Then the slope of the perpendicular line is -1/(-4), that is 1/4.