FIND MISSING ANGLES IN RHOMUS

Find the value of x in each rhombus :

Problem 1 :

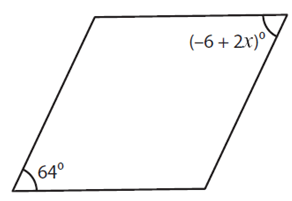
Solution :

By observing the figure,

The opposite angles in a rhombus are equal.

(-6 + 2x)^º = 64^º

-6 + 2x = 64

2x = 64 + 6

2x = 70

x = 70/2

x = 35

Problem 2 :

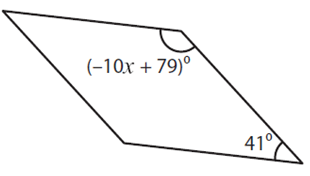
Solution :

By observing the figure,

The sum of angles of a linear pair is always equal to 180^º.

(-10x + 79) + 41 = 180

-10x + 79 + 41 = 180

-10x + 120 = 180

-10x = 180 - 120

x = -60/10

x = -6

Problem 3 :

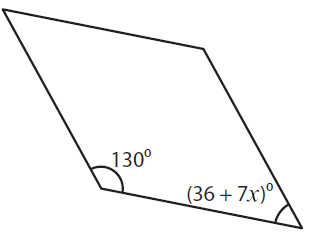
The sum of angles of a linear pair is always equal to 180.

130 + (36 + 7x) = 180

130 + 36 + 7x = 180

166 + 7x = 180

7x = 180 – 166

7x = 14

x = 14/7

x = 2

Problem 4 :

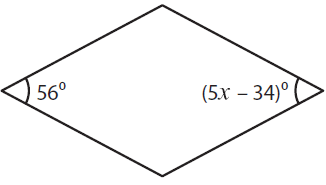
Solution :

The opposite angles in a rhombus are equal.

56 = (5x – 34)

56 = 5x – 34

56 + 34 = 5x

90 = 5x

90/5 = x

18 = x

Problem 5 :

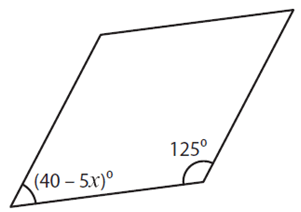
Solution :

The sum of angles of a linear pair is always equal to 180.

 (40 - 5x) + 125 = 180

40 – 5x + 125 = 180

165 – 5x = 180

-5x = 180 – 165

-5x = 15

x = -15/5

x = -3

Problem 6 :

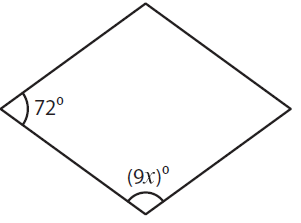
Solution :

The sum of angles of a linear pair is always equal to 180.

72 + 9x = 180

9x = 180 – 72

9x = 108

x = 108/9

x = 12

Problem 7 :

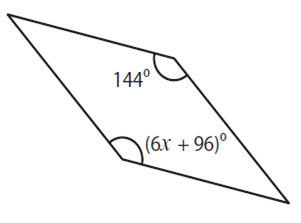
Solution :

The opposite angles in a rhombus are equal.

144^º = (6x + 96)^º

144^º = 6x^º + 96^º

144 - 96 = 6x

48 = 6x

48/6 = x

8 = x

Problem 8 :

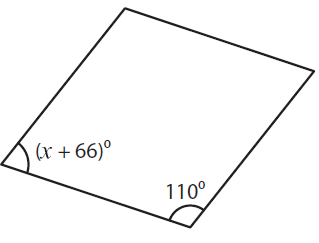
Solution :

The sum of angles of a linear pair is always equal to 180.

(x + 66) + 110 = 180

x + 66 + 110 = 180

x + 176 = 180

x = 180 – 176

x = 4