FIND LATERAL AND TOTAL SURFACE AREA OF CONE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is cone ?
A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of base) called the apex or vertex.
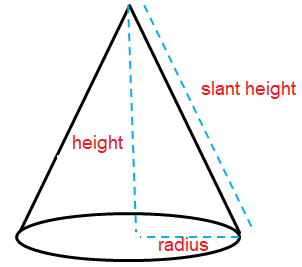
We can also define the cone as a pyramid which has a circular cross-section, unlike pyramid which has a triangular cross-section. These cones are also stated as a circular cone.
To find lateral surface area and total surface area of cone, we use the formulas given below.
Lateral surface area = πrl
Total surface area = πrl + πr2
= πr(l + r)
l = √r2 + h2
Here r = radius, l = slant height
Find
(i) Lateral surface area
(ii) Total surface area of the following cones given below.
Problem 1 :
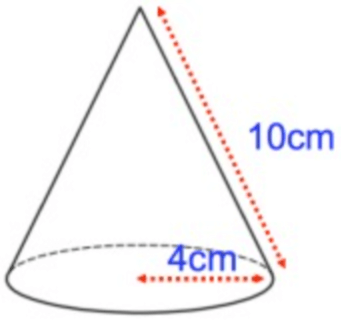
Solution :
(i) Lateral surface area = πrl
here radius (r) = 4 cm and slant height(l) = 10 cm
Lateral surface area = πrl
= π(4) (10)
= 40π cm2
(ii) Total surface area = πr(l + r)
= π(4)(10 + 4)
= 56π cm2
Problem 2 :
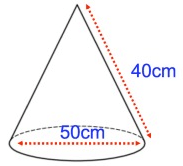
Solution :
(i) Lateral surface area = πrl
diameter = 50 cm, radius (r) = 25 cm, slant height (l) = 40 cm
= π(25) (40)
= 1000π cm2
(ii) Total surface area = πr(l + r)
= π(25)(40 + 25)
= 25π(65)
= 1625π cm2
Problem 3 :
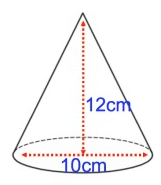
Solution :
(i) Lateral surface area = πrl
diameter = 10 cm, radius (r) = 5 cm, height (h) = 12 cm
l = √52 + 122
l = √25 + 144
l = √169
l = 13
= π(5) (13)
= 65π cm2
(ii) Total surface area = πr(l + r)
= π(5)(13 + 5)
= 5π(18)
= 90π cm2
Problem 4 :
The cone and cube below have the same surface areas. Workout the side length of cube x.
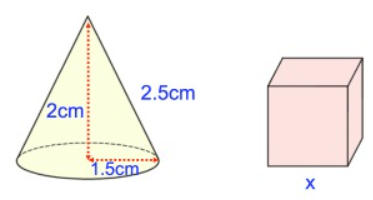
Solution :
Surface area of cone = surface area of cube
πrl = 4a2
From cone, r = 1.5 cm, h = 2 cm and l = 2.5 cm
π(1.5)(2.5) = 4x2
3.75π = 4x2
x2 = 0.9375π
Here π = 3.14
x2 = 0.9375(3.14)
x2 = 2.94375
x = 1.71
Problem 5 :
A paper cup shaped like a cone and has a diameter of 6 cm and slant height of 7.5 cm. How much paper is need to make the cup ?
Solution :
Since the paper cup will be open at the bottom, it is enough to find paper used to cover lateral surface.
Quantity of paper required = πrl
r = 6/2 ==> 3 cm and slant height (l) = 7.5
= π(3) (7.5)
Here π = 3.14
= 3.14 (22.5)
= 70.65 cm2
Quantity of paper required is 70.65 cm2.
Problem 6 :
The roof is shaped like a cone with the diameter of 12 feet. One bundle of shingles cover 32 square feet. How many bundles should you buy to cover the roof.
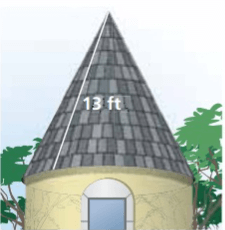
Solution :
Radius = 6 ft, slant height (l) = 13 ft
Area to be covered = πrl
= π(6) (13)
= 78π
Here π = 3.14
= 78(3.14)
= 244.92 ft2
One bundle of shingles cover 32 square feet
Number of shingles required = 244.92/32
= 7.65
So, approximately 8 bundles are needed.
Problem 7 :
Two Florida Atlantic University stickers are placed on opposite sides of megaphone. Estimate the percent of the surface area of the megaphone covered by the stickers. Round the answer to the nearest percent.
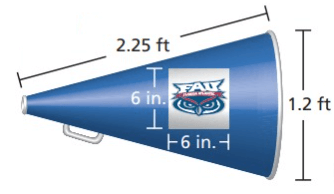
Solution :
Surface area of megaphone = πrl
r = 1.2/2 ==> 0.6 ft ==>7.2 inches
l = 2.25 ft ==> 27 inches
Applying in the formula, we get
= 3.14 (7.2)(27)
= 610.416 square inches
Area of sticker = 62 ==> 36 square inches
Area of two stickers = 72 square inches
Area covered by two sticker in total area
= (72/610.416) x 100%
= 11.79
= 12%
Problem 8 :
The cylinder and cone has the same surface area. Express L in terms of x.

Solution :
Surface area of cylinder = surface area of cone
2πrh = πrl
Radius of cylinder = radius of cone = x
height of cylinder = 3x and slant height of cone = l
2h = l
2(3x) = l
l = 6x
So, the value of l in terms of x is 6x.
Problem 9 :
A cone and cylinder are joined to make a solid. Find the total surface area.
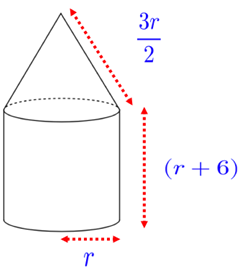
Solution :
Total surface area of figure = surface area of cylinder + surface area of cone
= 2πrh + πrl
radius = r, height of cylinder = r + 6 and slant height = 3r/2
Applying these values in the formula, we get
= πr[2h + l]
= π(r)[2(r + 6) + (3r/2)]
= πr[2r + 12 + (3r/2)]
= πr[(4r + 24 + 3r)/2]
= πr[(7r + 24)/2]
= πr/2 (7r + 24) square units.
So, the total surface area is πr/2 (7r + 24) square units.
Problem 10 :
You design a party hat. You attach a piece of elastic along a diameter.
(a) How long is the elastic?
(b) How much paper do you need to make the hat?

Solution :
Circumference of base = 22 inches
2πr = 22
2 x 22/7 x r = 22
r = 22 x 1/2 x 7/22
r = 3.5
Diameter = 2(3.5) ==> 7 inches
slant height = 5 inches
Surface area = πrl
= 3.14 x 3.5 x 5
= 54.95
Approximately 55 square inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling