FIND INVERSE OF LOGARITHMIC FUNCTION

If ƒ is a one-to-one function with domain D and range R, then the inverse function of ƒ, denoted by f^-1, is the function with domain R and range D defined by

ƒ^-1(b) = a if and only if ƒ(a) = b

To find inverse of a logarithmic function, we follow the steps given below.

Step 1 :

Replace f(x) by y.

Step 2 :

Derive the function for x.

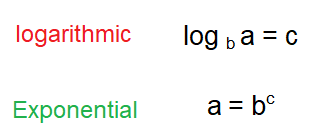
Step 3 :

Replace x by f^-1(x) and y by x.

Find the inverse of each of the following functions.

Example 1 :

f(x) = log₂(x - 3) - 5

Solution :

Example 2 :

f(x) = 3 log₃(x + 3) + 1

Solution :

Example 3 :

f(x) = -2 log 2(x - 1) + 2

Solution :

Example 4 :

f(x) = -ln(1 - 2x) + 1

Solution :

Example 5 :

f(x) = 2^x - 3

Solution :

Let y = f(x)

y = 2^x - 3

Add 3 on both sides

y + 3 = 2^x

log₂(y + 3) = x

f^-1(x) = log₂(x + 3)

Example 6 :

f(x) = 2 ⋅3^3x - 1

Solution :

Example 7 :

f(x) = -5 ⋅e^x + 2

Solution :

y = -5 ⋅e^x + 2

y - 2 = -5 ⋅e^x

2 - y = 5e^x

(2 - y)/5 = e^x

x = ln [(2 - y)/5]

f^-1(x) = ln [(2 - x)/5]

Example 8 :

f(x) = 1 - 2 ⋅e^-2x

Solution :

y = 1 - 2 ⋅e^-2x

2 ⋅e^-2x = 1 - y

e^-2x = (1 - y)/2

-2x = ln [(1 - y)/2]

x = (-1/2) ln [(1 - y)/2]

f^-1(x) = (-1/2) ln [(1 - x)/2]

Example 9 :

The wind speed s (in miles per hour) near the center of a tornado can be modeled by s = 93 log d + 65, where d is the distance (in miles) that the tornado travels.

a. In 1925, a tornado traveled 220 miles through three states. Estimate the wind speed near the center of the tornado.

b. Find the inverse of the given function. Describe what the inverse represents

Solution :

s = 93 log d + 65

Here d is the distance (in miles) that the tornado travels.

s is the wind speed s (in miles per hour)

a) When d = 220 miles, s = ?

s = 93 log 220 + 65

s = 93(2.342) + 65

= 217.806 + 65

= 282.806

So, the required speed 283 miles per hour.

b) 

s = 93 log d + 65

s - 65 = 93 log d

(s - 65)/93 = log d

d = 10^{(s - 65)/93}

The function represents distance traveled with the speed of s miles per hour.