FIND INCREASING AND DECREASING INTERVALS OF ABSOLUTE VALUE FUNCTIONS

To find increasing and decreasing interval of absolute value function, first we should find the vertex. Because vertex is the turning point of the curve.

We know that graphing form of absolute value function will have the shape V. It may be V or inverted V, based on the sign of coefficient of absolute value function, we will decide.

If the curve opens up,

• to the left of vertex, it is decreasing. To the right of vertex, it is increasing.

If the curve opens down,

• to the left of vertex, it is increasing. To the right of vertex, it is decreasing.

To get more examples to know how to graph absolute value function, please visit the pages given.

• Graphing absolute value function
• How to sketch absolute value function

Problem 1 :

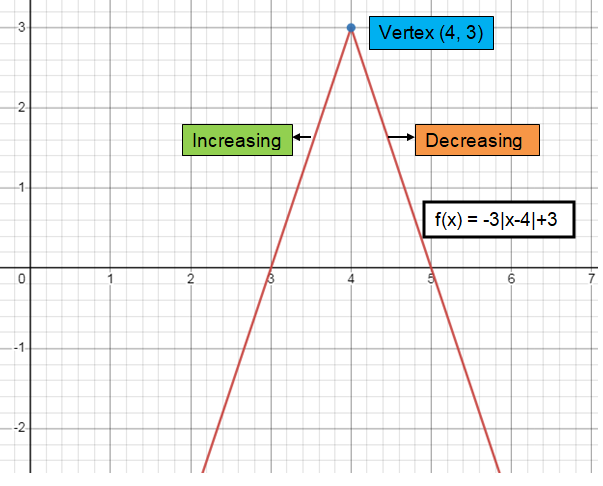
f(x) = -3│x - 4│ + 3

Solution :

a = -3, h = 4, k = 3

Vertex:

f(x) = -3│x - 4│ + 3

Comparing with f(x) = a |x - h|+ k

Vertex (h, k) = (4, 3)

Slope :

Slope (a) = -3

The curve will open down.

y- intercept :

y- Intercept, put x = 0

y = -3│0 - 4│ + 3

y = -3(4) + 3

y = -12 + 3

y = -9

y- Intercept = (0, -9)

Zeros :

x- Intercept, put y = 0

 -3│x - 4│ + 3 = 0

-3│x - 4│= -3

│x - 4│= -3/-3

│x - 4│= 1

x = 1 + 4

x = 5

x- Intercept is (5, 0)

Domain and range :

• All real value is domain.
• Range is [3, -∞)

Increasing and decreasing :

• To the left of maximum, it is increasing. (-∞, 4)
• To the right of maximum, it is decreasing. (4, ∞)

Problem 2 :

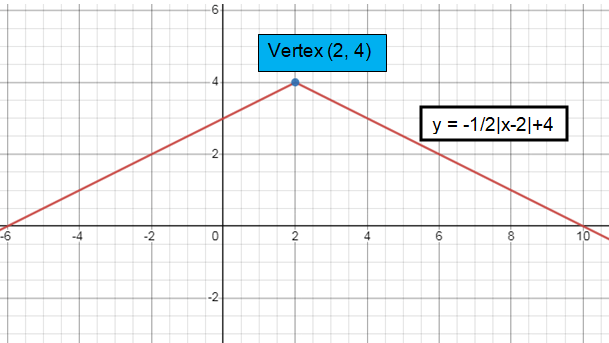
f(x) = -1/2│x - 2│ + 4

Solution :

a = -1/2, h = 2, k = 4

Vertex :

f(x) = -1/2│x - 2│ + 4

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) = (2, 4)

Slope :

Slope (a) = -1/2

The curve will open down.

y- intercept :

y- Intercept, put x = 0

y = -1/2│0 - 2│ + 4

y = -1/2(2) + 4

y = -1 + 4

y = 3

y- Intercept = (0, 3)

Zeros :

x- Intercept, put y = 0

 -1/2│x - 2│ + 4 = 0

-1/2│x - 2│= -4

│x - 2│= -4(-2)

│x - 2│= 8

x = 8 + 2

x = 10

x- Intercept is (10, 0)

Domain and range:

• All real value is domain.
• Range is (-∞, 4]

Increasing and decreasing:

• To the left of maximum, it is increasing. (-∞, 2]
• To the right of maximum, it is decreasing. [2, ∞)

Problem 3 :

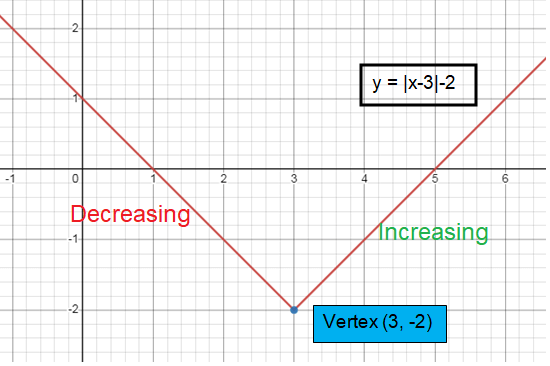
f(x) = │x - 3│ - 2

Solution :

a = 1, h = 3, k = -2

Vertex :

f(x) = │x - 3│ - 2

Comparing with f(x) = a│x - h│+ k

Vertex (h, k) is (3, -2)

Slope :

Slope (a) = 1

The curve will open up.

y- intercept :

y- Intercept, put x = 0

y = │0 - 3│ - 2

y = 3 - 2

y = 1

y- Intercept = (0, 1)

Zeros :

x- Intercept, put y = 0

 │x - 3│ - 2 = 0

│x - 3│= 2

x = 2 + 3

x = 5

x- Intercept = (5, 0)

Domain and range :

• All real value is domain.
• Range is [-2, ∞)

Increasing and decreasing :

• To the right of minimum, it is increasing. (∞, 3]
• To the left of minimum, it is decreasing. [3,-∞)