FIND HIGHEST COMMON FACTOR OF TWO NUMBERS LADDER METHOD

Find the highest common factor of the following.

Problem 1 :

12 and 15

Solution :

Considering the given numbers 12 and 15, both are multiples of 3. So, they are divisible by 3.

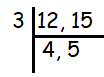
Here 4 and 5 cannot be divided by any times table. So, the highest common factor is 3.

Problem 2 :

16 and 20

Solution :

Since 16 and 20 are even numbers, both are divisible by 2.

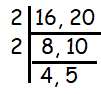
Highest common factor = 2 x 2

= 4

Problem 3 :

21 and 35

Solution :

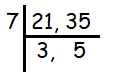
3 and 5 are not divisible by any other same times table. Multiplying the common divisors, we get

So, the highest common factor is 7.

Problem 4 :

16 and 56

Solution :

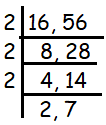
Since 16 and 56 are even numbers, we can divide both by 2. From the above shown work, it is clear that 2 and 7 cannot be divided any times table.

Multiplying the common divisors, we get

= 2 x 2 x 2

= 8

So, the highest common factor is 8.

Problem 5 :

20 and 36

Solution :

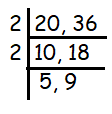
Since 20 and 36 are even numbers, we divide both by using 2 times table. 

5 and 9 are not divisible by same times table. Then multiplying the divisors, we get

= 2 x 2

= 4

Highest common factor = 4

Problem 6 :

18 and 45

Solution :

Divisibility rule for 2 :

Here 18 is even 45 is odd. Then, we cannot use 2 times table to divide it.

Divisibility rule for 3 :

Sum of the digits of 18 is 9 and sum of the digits of 45 is also 9. Then both are divisible by 3.

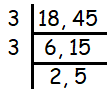
Multiplying the common divisors, we get

= 3 x 3

= 9

So, the highest common factor is 9.

Problem 7 :

40 and 46

Solution :

Since 40 and 46 are even numbers, they are divisible by 2. By observing the last step 20 and 23 is not divisible by same times table.

Then, highest common factor is 2.

Problem 8 :

44 and 110

Solution :

Since 44 and 110 are even numbers, they are divisible by 2. In the next step, we have 22 and 55 and they are divisible by 11.

At last we have 2 and 5, they are not divisible by same times table. By multiplying the common factors, we get

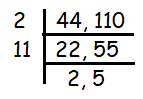
= 2 x 11

= 22

So, the highest common factor is 22.

Problem 9 :

81 and 108

Solution :

Divisibility by 2 :

Here 81 is odd number and 108 is even number. So, both are not divisible by 2.

Divisibility by 3 :

Sum of the digits of 81 is 9, sum of the digits of 108 is 9. So, both are divisible by 3.

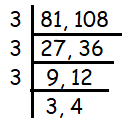
At last 3 and 4 are co primes, so cannot divided by any common times table. Multiplying the common divisors,

= 3 x 3 x 3

= 27

So, the highest common factor is 27.

Problem 10 :

135 and 360

Solution :

Divisibility by 5 :

Here 135 and 360 ends with 5 and 0 respectively, then they are divisible by 5.

Divisible by 3 :

Sum of the digits in 27 is 9. The sum of the digits in 72 is 9. Then both are divisible by 3.

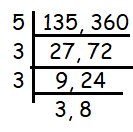
At last 3 and 8 are not divisible by same times table. Multiplying the common factors, we get

= 5 x 3 x 3

= 45

So, the highest common factor is 45.

Problem 11 :

Ed has two lengths of network cable, one measuring 18 m and other measuring 12 m. He wishes to cut them into shorter cables which are all the same lengths. What is the longest length of cable Ed can make in this way ?

Solution :

Length of two network cables are 18 m and 12 m.

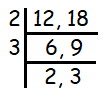
Since 12 and 18 are even numbers, they are divisible by 2. Continue dividing it by 3, we get 2 and 3 at last. These two numbers are coprime, it cannot be divisible further. Then, multiplying the common factors, we get

= 2 x 3

= 6 is the highest common factor.

So, cables can be cut into 6 m length of short cables.

Problem 12 :

A hardware store  nails in packets which all contain the same number of nails. Ron bought a total of 320 nails and Tess bought a total of 200 nails. Which is the greatest possible number of nails that could be in each packet ?

Solution :

Number of nails in the packet that Ron has = 320

Number of nails in the packet that Tess has = 200

Both are even numbers, they are divisible by 2 and 5.

Multiplying the common factors, we get

= 5 x 2 x 2 x 2

= 40

So, the greatest number of nails in each packet is 40.