FIND HEIGHT OF CYLINDER GIVEN SURFACE AREA

Work out the height of each cylinder below.

Problem 1 :

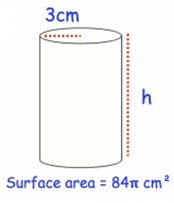
Solution :

Radius r = 3 cm, Height h = ?

Surface area (A) = 84π cm²

Surface area (A) = 2πr (h + r)

84π = 2π(3) (h + 3)

84π = 6π(h + 3)

Divide each side by 6π.

84π/6π = (6π(h + 3))/6π

14 = h + 3

14 – 3 = h

11 cm = h

Problem 2 :

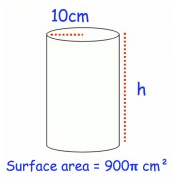
Solution :

Radius r = 10 cm and Height h = ?

Surface area A = 900π cm²

Surface area A= 2πr(h + r)

900π = 2π(10)(h + 10)

900π = 20π(h + 10)

Divide each side by 20π.

900π/20π = (20π(h + 10))/20π

45 = h + 10

45 – 10 = h

35 cm = h

Work out the radius of each cylinder below

Problem 3 :

If a cylinder has a surface area of 100 cm² and its height is 4 times the radius, what is the height of the cylinder ?

Solution :

Surface area of cylinder = 100 cm²

height = 4 (radius)

h = 4r

2πr(h + r) = 100

2πr(4r + r) = 100

2πr(5r) = 100

10πr² = 100

r² = 10/π

r = √(10/π)

height = 4√(10/π)

Problem 4 :

The radius and height of a cylinder are in the ratio 11 : 7. If the curved surface area of cylinder is 121 square cm. Find the radius and height of the cylinder.

Solution :

Radius of the cylinder = 11x and height of the cylinder = 7x

Surface area of cylinder = 121

2πrh = 121

2π 11x 7x = 121

Problem 5 :

The lateral surface area of a right circular cylinder of radius 3 cm is 94.2 cm². The height of the cylinder is ?

Solution :

Lateral surface area of cylinder = 94.2 cm²

2πrh = 94.2

2 x 3.14 x 3 x h = 94.2

h = 94.2/18.84

h = 5

So, height of the cylinder is 5 cm.

Problem 6 :

How much paper is used for the label on the can of peas ?

Find the lateral surface area of the cylinder ?

You earn $0.01 for recycling the can. How much can you expect to earn for recycling the tomato can? Assume that the recycle value is proportional to the surface area.

Solution :

Lateral surface area of cylinder = 2πrh

r = 1 inch and height = 2 inch

= 2 x 3.14 x 1 x 2

= 12.56

About 12.56 square inches of paper is used for the label.

Finding the total surface area of cylinder :

Surface area of peas tin :

= 2πrh + 2πr²

= 2πr(h + r)

= 2 x 3.14 x 1 (2 + 1)

= 6.28 x 3

= 18.84 square inches

Surface area of tomatoes tin :

= 2πr(h + r)

= 2 x 3.14 x 2 (5.5 + 2)

= 12.56 x 7.5

= 94.2 square inches

Use a proportion to find the recycle value x of the tomato can.

94.2/18.84 = x/0.01

5 = x/0.01

x = 5(0.01)

x = 0.05

You can expect to earn $0.05 for recycling the tomato can.

Problem 7 :

The truck’s tank is a stainless steel cylinder. Find the surface area of the tank.

Solution :

Height = 50 ft and radius = 4 ft

Surface area of tank = 2πrh

= 2 x π x 4 x 50

= 400π square ft

Problem 8 :

Describe and correct the error in finding the surface area of the cylinder

Solution :

r = 6 ft and h = 11 ft

Surface area = 2πr(h + r)

= 2 x π x 6 (6 + 11)

= 12π(17)

= 204π square ft

Problem 9 :

What percent of the surface area of the ottoman is green (not including the bottom)?

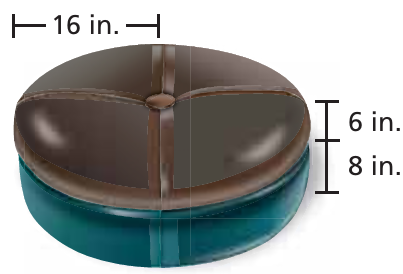
Solution :

Surface area of brown part = πr² + 2πrh

= πr(r + 2h)

= π x 16 (16 + 2(6))

= 16π(16 + 12)

= 16π(28)

= 448π

Surface area of green part = 2πrh

= 2π x 16 x 8

= 256π

Total area = 448π + 256π

= 704π

Percentage of green = (256π/704π) x 100%

= 0.3636...... x 100%

= 36.36%

Problem 10 :

You make two cylinders using 8.5-inch by 11-inch pieces of paper. One has a height of 8.5 inches and the other has a height of 11 inches. Compare the surface areas of the cylinders.

Solution :

Surface area of first cylinder :

When height of the cylinder = 8.5 inches, circumference of the circular base = 11 inches

2πr = 11

Surface area = 2πrh

= 11(8.5)

= 93.5

Surface area of second cylinder :

When height of the cylinder = 11 inches, circumference of the circular base = 8.5 inches

2πr = 8.5

Surface area = 2πrh

= 8.5(11)

= 93.5

So, both cylinders will have the same surface area.