FIND GREATEST FOUR DIGIT NUMBER WHICH IS DIVISIBLE BY GIVEN NUMBERS

Problem 1 :

Find the largest four digit number exactly divisible by 12, 15, 18 and 27.

Solution :

The largest four digit number is 9999.

Since the required four digit number exactly divisible by 12, 15, 18 and 27, the required number is divisible by the given numbers.

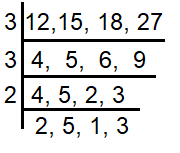
LCM (12, 15, 18 and 27) = 54 x 10 ==> 540

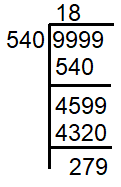
9999 - 279 = 9720

9720 is the largest four digit number which is divisible by 12, 15, 18 and 27.

Problem 2 :

The largest four digit number which when divided by 4, 7 or 13 leaves the remainder of 3 in each case.

Solution :

LCM of 4, 7 and 13 = 364

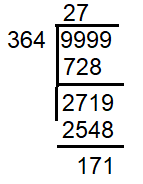
9999 - 171 ==> 9828

When we divide 9828 by 4, 7 and 13, we will get 0 as remainder. But accordingly the question, we should get 3 as remainder.

So, the required number 3 greater than 9828.

required number = 9828 + 3

= 9831

Problem 3 :

The greatest number of four digits which is divisible by 15, 25, 40 and 75 is :

Solution :

LCM (15, 25, 40, 75)

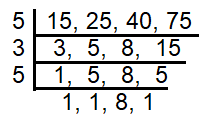
LCM (15, 25, 40, 75) = 600

The greater four digit number = 9999

Divide 9999 by 600

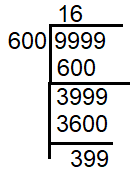
9999 - 399 ==> 9600

So, the required greatest four digit number which is divisible by 15, 25, 40 and 75 is 9600.