FIND EXPANSION USING THREE BASIC ALGEBRAIC IDENTITIES

Expand the following using algebraic identities given above.

Problem 1 :

(2x + y)²

Solution :

Here a = 2x and b = y

It looks like (a + b)²

= (2x)² + 2(2x) y + y²

= 2²x² + 2(2x) y + y²

= 4x² + 4xy + y²

Problem 2 :

(3a + 2b)²

Solution :

a = 3a and b = 2b

It looks like (a + b)²

= (3a)² + 2(3a) (2b) + (2b)²

= 3²a² + 12ab + 2²b²

= 9a² + 12ab + 4b²

Problem 3 :

(x² + 2)²

Solution :

a = x² and b = 2

It looks like (a + b)²

= (x²)² + 2(x²) (2) + 2²

= x⁴ + 4x² + 4

Problem 4 :

(√2 + x)²

Solution :

a = √2 and b = x

It looks like (a + b)²

= (√2)² + 2(√2) (x) + x²

= 2 + 2√2x + x²

Problem 5 :

(x - 1/x)²

Solution :

a = x and b = 1/x

It looks like (a - b)²

= x² - 2x (1/x) + (1/x)²

= x² - 2 + (1/x²)

Problem 6 :

(2 - x²)²

Solution :

a = 2 and b = x²

It looks like (a - b)²

= 2² - 2(2) (x²) + (x²)²

= 4 - 4x² + x⁴

Problem 7 :

(8y - 5z)²

Solution :

a = 8y and b = 5z

It looks like (a - b)²

= (8y)² - 2(8y) (5z) + (5z)²

= 8²y² - 16y (5z) + 5²z²

= 64y² - 80yz + 25z²

Problem 8 :

x² - 9

Solution :

Here 9 = 3²

x² - 9 = x² - 3²

It looks like a² - b²

Here a = x and b = 3

x² - 9 = (x + 3) (x - 3)

Problem 9 :

x²y² - 1

Solution :

= x²y² - 1

= (xy)² - 1²

= (xy + 1) (xy - 1)

Problem 10 :

3x² - 27y²

Solution :

= 3x² - 27y²

Factoring 3, we get

= 3(x² - 9y²)

= 3 (x² - 3²y²)

= 3(x² - (3y)²)

= 3(x + 3y) (x - 3y)

Problem 11 :

400x² - 169y²

Solution :

= 400x² - 169y²

We cannot factorize anything.

400 = 20² and 169 = 13²

= ((20x)² - (13y)²)

= (20x + 13y) (20x - 13y)

Problem 12 :

(a+b)² - c²

Solution :

Here a = a + b and b = c

Using the algebraic identity a² - b², we get

= (a + b + c) (a + b - c)

Problem 13 :

(3x + 1)² - 9

Solution :

= (3x + 1)² - 9

= (3x + 1)² - 3²

Here a = 3x + 1 and b = 3

= (3x + 1 + 3) (3x + 1 - 3)

= (3x + 4) (3x - 2)

Write a polynomial that represents the area of the square.

Problem 14 :

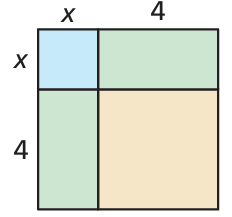
Solution :

Side length of square = x + 4

Area od square = side (side)

= (x + 4)(x + 4)

= (x + 4)²

Using the algebriac identity (a + b)² = a² + 2ab + b²

= x² + 2x(4) + 4²

= x² + 8x + 16

Problem 15 :

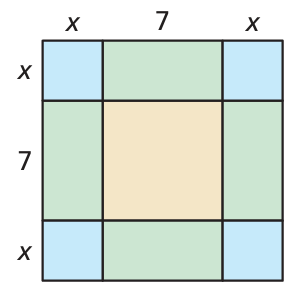
Solution :

Side length of square = x + x + 7

= 2x + 7

Area od square = side (side)

= (2x + 7)(2x + 7)

= (2x + 7)²

Using the algebriac identity (a + b)² = a² + 2ab + b²

= (2x)² + 2(2x)7 + 7²

= 2²x² + (4x)7 + 7²

= 4x² + 28x + 49

= x² + 8x + 16

Problem 16 :

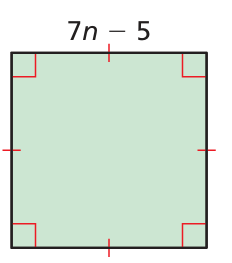
Solution :

Side length of square = 7n - 5

Area od square = side (side)

= (7n - 5)(7n - 5)

= (7n - 5)²

Using the algebriac identity (a - b)² = a² - 2ab + b²

= (7n)² - 2(7n)5 + 5²

= 7²n² - (14n)5 + 25

= 49n² - 70n + 25

Problem 17 :

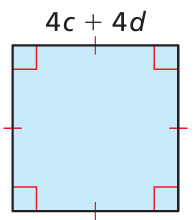
Solution :

Side length of square = 4c + 4d

Area od square = side (side)

= (4c + 4d)(4c + 4d)

= 4(c + d) 4(c + d)

= 16(c + d)²

Using the algebriac identity (a + b)² = a² + 2ab + b²

= 16[c² - 2cd + d²]

= 16c² - 32cd + 16d²

Problem 18 :

Find k so that 9x² − 48x + k is the square of a binomial.

Solution :

= 9x² − 48x + k

= 3²x² - 2(24x) + k

= (3x)² - 2(3x)(4) + k

(3x)² - 2(3x)(4) + k = (3x)² - 2(3x)(4) + 2²

(3x)² - 2(3x)(4) + k = (3x + 2)²

Comparing the corresponding terms, we get k = 4.

Problem 19 :

Write two binomials that have the product x² − 121. Explain

Solution :

= x² − 121

= x² − 11²

Using the algebraic identity, a² - b² = (a + b)(a - b)

= (x + 11)(x - 11)

So, the binomials are (x + 11)(x - 11).

Problem 20 :

You are making a blanket with a fringe border of equal width on each side.

a. Write a polynomial that represents the perimeter of the blanket including the fringe.

b. Write a polynomial that represents the area of the blanket including the fringe.

c. Find the perimeter and the area of the blanket including the fringe when the width of the fringe is 4 inches.

Solution :

Length = 72 + x + x

= 72 + 2x

Width = 48 + x + x

= 48 + 2x

a) Perimeter of blanket = 2(lenght + wdith)

= 2(72 + 2x + 48 + 2x)

= 2(120 + 4x)

= 240 + 8x

b) Area including fringe = length x width

= (72 + 2x)(48 + 2x)

= 3456 + 144x + 96x + 4x²

= 3456 + 240x + 4x²

c) When x = 4

Perimeter = 240 + 8(4)

= 240 + 32

= 272 inches

When x = 4

Area = 3456 + 240x + 4x²

= 3456 + 240(4) + 4(4)²

= 3456 + 960 + 64

= 4480 square inches