FIND EQUATION OF THE LINE PERPENDICULAR TO GIVEN LINE

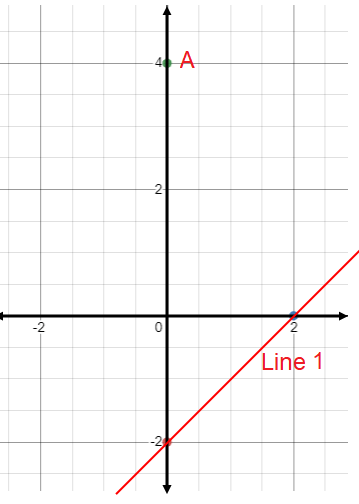
Write down the equation of the line perpendicular to the line 1 and passing through A.

Problem 1 :

Solution :

Choosing two points from the line (0, -2) and (2, 0).

Slope (m) = (0 + 2)/(2 - 0)

m = 2/2

m = 1

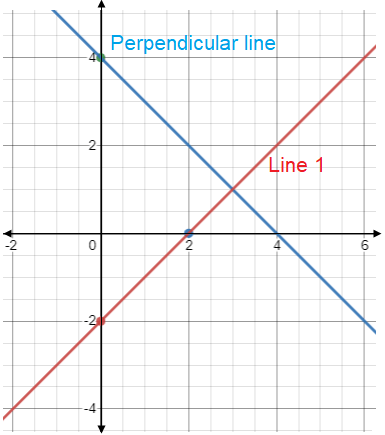
Slope of the perpendicular line, which passes through the point A is -1.

Equation of the line passes through A (0, 4) is :

y - 4 = -1(x - 0)

y - 4 = -x

y = -x + 4

So, equation of the required line is y = -x + 4.

Problem 2 :

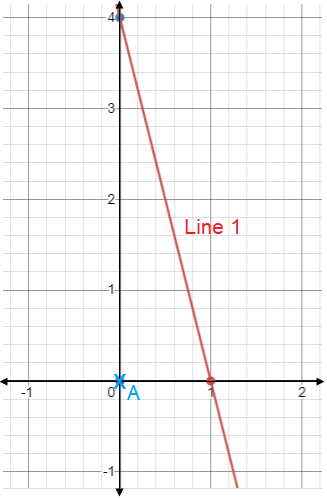
Solution :

Choosing two points from the line (1, 0) and (0, 4).

Slope (m) = (4 - 0)/(0 - 1)

m = 4/(-1)

m = -4

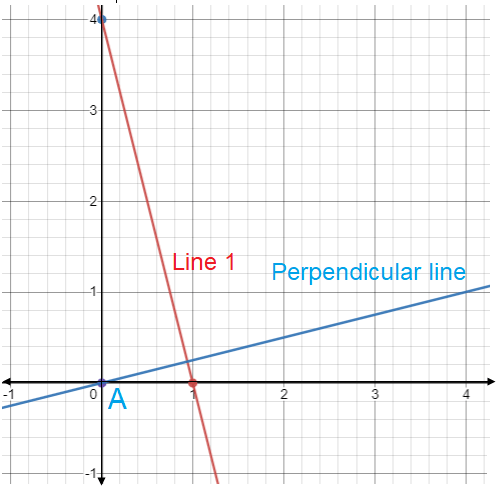
Slope of the perpendicular line, which passes through the point A is 1/4.

Equation of the line passes through A (0, 0) is :

y - 0 = (1/4)(x - 0)

y = x/4

So, equation of the required line is y = x/4.

Problem 3 :

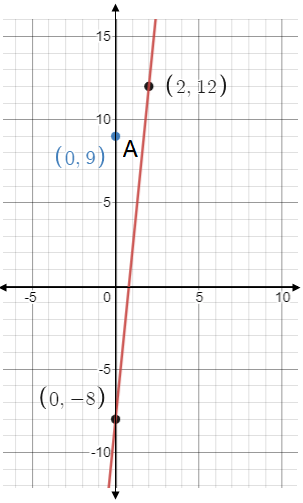
Solution :

Choosing two points from the line (0, -8) and (1, 2).

Slope (m) = (2 - (-8))/(1 - 0)

m = (2+8)/1

m = 10

Slope of the perpendicular line, which passes through the point A is -1/10.

Equation of the line passes through A (0, 9) is :

y - 9 = (-1/10)(x - 0)

10(y - 9) = -x

10y - 90 =-x

y = (-1/10)x + (90/10)

y = (-1/10)x + 9

So, equation of the required line is y = (-1/10)x + 9.

Problem 4 :

Find the equation of the line that is perpendicular to y = (2/3)x + 3 and paases through the point (12, -1).

Solution :

y = (2/3)x + 3

Comparing the given equation with y = mx + b

Slope of the given line = 2/3

Slope of the perpendicular line = -1/(2/3)

= -3/2

Equation of the perpendicular line :

(y - y₁) = m(x - x₁)

(y - (-1)) = (-3/2) (x - 12)

(y - (-1)) = (-3/2) (x - 12)

2(y + 1) = -3(x - 12)

2y + 2 = -3x + 36

3x + 2y = 36 - 2

3x + 2y = 34

Problem 5 :

Line A passes through the points (1, 2) and (5, 18).

Line B passes through the points (7, 3) and (9, 11).

Are lines A and B parallel, perpendicular or neither?

Solution :

Slope of the line passes through the points (1, 2) and (5, 18).

m₁ = (18 - 2) / (5 - 1)

= 16/4

= 4

Slope of the line passes through the points (7, 3) and (9, 11).

m₂ = (11 - 3) / (9 - 7)

= 8/2

= 4

Since the slopes are equal, then the lines are parallel.

Problem 6 :

Line A passes through the points (-3, -1) and (-1, 9) Line B passes through the points (-2, 1) and (k, 4) Line A and Line B are perpendicular. Find the value of k.

Solution :

(-3, -1) and (-1, 9)

Slope of the line A = (9 - (-1)) / (-1 - (-3))

= (9 + 1)/(-1 + 3)

= 10 / 2

= 5

(-2, 1) and (k, 4)

Slope of the line A = (4 - 1) / (k - (-2))

= 3 / (k + 2)

5 [3/(k + 2)] = -1

15 / (k + 2) =  -1

15 = -(k + 2)

15 = -k - 2

k = -2 - 15

k = -17

So, the value of k is -17.

Problem 7 :

X = (3, 10) Y = (-5, 8) Z = (5, 5) Find the equation of the line perpendicular to XZ that passes through point Y.

Solution :

Slope of the line passes through points X(3, 10) Z (5, 5)

= (5 - 10) / (5 - 3)

= -5/3

Slope of the perpendicular line = -1/(-5/3)

= 3/5

Equation of the line passes through the point Y :

(y - y₁) = m(x - x₁)

y - 8 = (3/5) (x - (-5))

5(y - 8) = 3(x + 5)

5y - 40 = 3x + 15

3x - 5y = -40 - 15

3x - 5y = -55

Problem 8 :

Pictured to the right is a straight line L and points P and Q.

(a) Find the equation of the line L.

(b) Find the equation of the line that is parallel to L and passes through P.

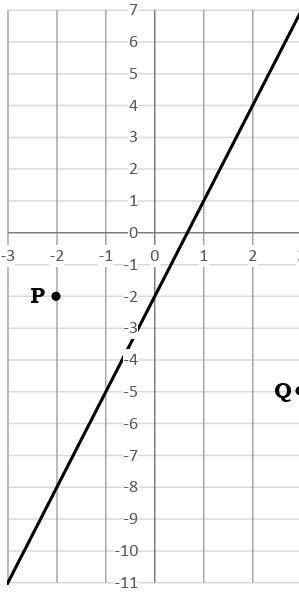
Solution :

a)  Equation of line L :

Points on the line (0, -2) (-1, -5)

= (-5 - (-2)) / (-1 - 0)

= (-5 + 2) / (-1)

= 3

(y - y₁) = m(x - x₁)

(y - (-2)) = 3(x - 0)

y + 2 = 3x

3x - y - 2 = 0

b)

Slope of the perpendicular line P :

P(-2, -2)

Slope of the line P = -1/3

(y - (-2)) = (-1/3) (x - (-2))

(y + 2) = (-1/3) (x + 2)

3(y + 2) = -1(x + 2)

3y + 6 = -x - 2

x + 3y = - 2 - 6

x + 3y = -8