FIND EQUATION OF THE LINE IN SLOPE INTERCEPT FORM

Find the equation of the line in slope intercept form with the given information.

Problem 1 :

m = -2 and goes through (-1, 4)

Solution :

Equation of the line passes through the point and slope 

y - y₁ = m(x - x₁)

Here (x₁, y₁) is (-1, 4) and slope (m) = -2

(y - 4) = -2(x - (-1))

y - 4 = -2(x + 1)

y - 4 = -2x - 2

y = -2x - 2 + 4

y = -2x + 2

So, the required equation in slope intercept form is

y = -2x + 2

Problem 2 :

Goes through (1, 4) and (3, 10)

Solution :

Equation of the line passes through the point and slope 

y - y₁ = m(x - x₁) -----(1)

Here (x₁, y₁) is (1, 4) and (x₂, y₂) is (3, 10)

m = (y₂ - y₁)/(x₂ - x₁)

m = (10 - 4) / (3 - 1)

= 6/2

m = 3

Applying any one of the points given and slope in (1), we get

y - 1 = 3(x - 4)

y = 3x - 12 + 1

y = 3x - 11

Problem 3 :

Goes through (-4, -5) and (-1, -1)

Solution :

Equation of the line passes through the point and slope 

y - y₁ = m(x - x₁) -----(1)

Here (x₁, y₁) is (-4, -5) and (x₂, y₂) is (-1, -1)

m = (y₂ - y₁)/(x₂ - x₁)

m = (-1 + 5) / (-1 + 4)

m = 4/3

Applying any one of the points given and slope in (1), we get

y + 1 = (4/3) (x + 1)

3(y + 1) = 4(x + 1)

3y + 3 = 4x + 4

4x - 3y + 4 - 3 = 0

4x - 3y + 1 = 0

Problem 4 :

Goes through (3, 7) and (3, 9)

Solution :

y - y₁ = m(x - x₁) -----(1)

Here (x₁, y₁) is (3, 7) and (x₂, y₂) is (3, 9)

m = (y₂ - y₁)/(x₂ - x₁)

m = (9 - 7) / (3 - 3)

m = 2/0

m = infinity

It must be a vertical line.

Applying any one of the points given and slope in (1), we get

y - 7 = (2/0) (x - 3)

0(y - 7) = 2(x - 3)

0 = 2(x - 3)

x = 3 is the required vertical line.

Problem 5 :

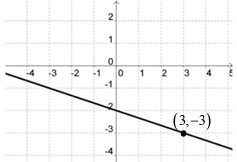
Solution :

From the graph given above, it is clear that y-intercept is at -2 and the point is (3, -3).

y = mx + b

y = -2x + b ---(1)

Applying the point (3, -3), we get

-3 = -2(3) + b

-3 =  -6 + b

-3 + 6 = b

b = 3

Applying the value of b in (1), we get

y = -2x + 3

Problem 6 :

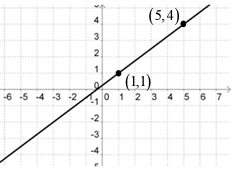
Solution :

Here (x₁, y₁) is (1, 1) and (x₂, y₂) is (5, 4)

m = (y₂ - y₁)/(x₂ - x₁)

m = (4 - 1) / (5 - 1)

= 3/4

Applying any one of the points given and slope in (1), we get

y - 1 = (3/4)(x - 1)

4(y - 1) = 3(x - 1)

4y - 4 = 3x - 3

3x - 4y - 3 + 4 = 0

3x - 4y + 1 = 0

Problem 7 :

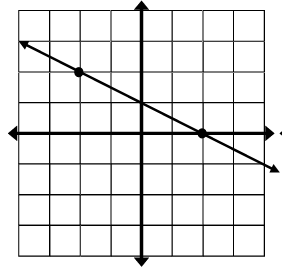
Solution :

By observing the graph given above, the line passes through two points.

Here (x₁, y₁) is (-2, 2) and (x₂, y₂) is (2, 0)

m = (y₂ - y₁)/(x₂ - x₁)

m = (0 - 2) / (2 + 2)

= -2/4

= -1/2

Applying any one of the points given and slope in (1), we get

y - 0 = (-1/2)(x - 2)

2(y - 0) = -1(x - 2)

2y = -x + 2

Converting into slope intercept form, we get

y = (-1/2)x + 1

Problem 8 :

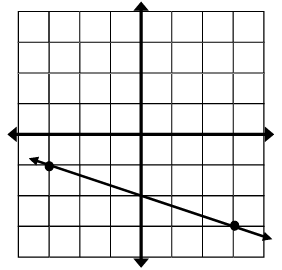
Solution :

By observing the graph given above, the line passes through two points.

Here (x₁, y₁) is (-3, -1) and y-intercept is -2

y + 1 = -2(x + 3)

y + 1 = -2x - 6

Converting into slope intercept form, we get

y = -2x - 6 - 1

y = -2x - 7