FIND EQUATION OF THE CIRCLES WITH GIVEN INFORMATION

Problem 1 :

Ends of diameter : (-17, -9) and (-19, -9).

Solution :

Where (h, k) = -18, -9

(x - h)² + (y - k)² = r²

 (x + 18)² + (y + 9)² = r² --- (1)

(-17, -9) substitute the equation (1).

 (-17 + 18)² + (-9 + 9)² = r²

1² = r²

r² = 1 substitute the equation (1).

 (x + 18)² + (y + 9)² = 1

Problem 2 :

Ends of diameter : (-3, 11) and (3, -13).

Solution :

Where h = 0 and k = -1

(x - h)² + (y - k)² = r²

 (x - 0)² + (y + 1)² = r²

x² + (y  + 1)² = r²--- (1)

(3, -13) substitute the equation (1).

 3² + (-13  + 1)² = r²

9 + (12)² = r²

153 = r²

r² = 153 substitute the equation (1).

 x² + (y + 1)² = 153

Problem 3 :

Center : (-15, 3√7), Area : 2π

Solution :

Equation of circle with center (h ,k) :

 (x - h)² + (y - k)² = r²

h, k is  -15, 3√7 

 (x + 15)² + (y - 3√7)² = r² --- (1)

Area of the circle = πr²

2π = πr²

r² = 2

r² = 2 substitute the equation (1).

 (x + 15)² + (y - 3√7)²  = 2

Problem 4 :

Center : (-11, -14), Area : 16π

Solution :

Equation of circle with center (h ,k) :

(x - h)² + (y - k)² = r²

Where h = -11 and k = -14

 (x + 11)² + (y + 14)² = r² --- (1)

Area of the circle = πr²

16π = πr²

r² = 16

r² = 16 substitute the equation (1).

 (x + 11)² + (y + 14)²  = 16

Problem 5 :

Center : (-5, 12), Circumference : 8π

Solution :

Equation of circle with center (h ,k) :

(x - h)² + (y - k)² = r²

Where h = -5 and k = 12

(x + 5)² + (y - 12)² = r² --- (1)

Area of the circle = 2πr

8π = 2πr

r = 4

r = 4 substitute the equation (1).

 (x + 5)² + (y - 12)²  = 4²

 (x + 5)² + (y - 12)²  = 16

Problem 6 :

Center : (15, 14), Circumference : 2π√15

Solution :

Equation of circle with center (h ,k) :

(x - h)² + (y - k)² = r²

Where h = 15 and k = 14

 (x - 15)² + (y - 14)² = r² --- (1)

Area of the circle = 2πr

2π√15 = 2πr

r = √15

r = √15 substitute the equation (1).

 (x - 15)² + (y - 14)²  = (√15)²

 (x - 15)² + (y - 14)²  = 15

Problem 7 :

Center : (2, -5), Point on circle : (-7, -1)

Solution :

Equation of circle with center (h ,k) :

(x - h)² + (y - k)² = r²

Where h = 2 and k = -5

 (x - 2)² + (y + 5)² = r² --- (1)

Point on circle r = √[(x₂ - x₁)² + (y₂ - y₁)]

(x₁, y₁) = (2, -5)

(x₂, y₂) = (-7, -1)

= √[(-7 - 2)² + (-1 + 5)²]

= √[(-9)² + (4)²]

=  √[81  +16]

r = √97

r = √96 substitute the equation (1).

 (x - 2)² + (y + 5)²  = (√96)²

 (x - 2)² + (y + 5)²  = 97

Problem 8 :

Center : (14, 17), Point on circle : (15, 17)

Solution :

Equation of circle with center (h ,k) :

(x - h)² + (y - k)² = r²

Where h = 14 and k = 17

 (x - 14)² + (y - 17)² = r² --- (1)

Point on circle r = √[(x₂ - x₁)² + (y₂ - y₁)²]

(x₁, y₁) = (14, 17)

(x₂, y₂) = (15, 17)

= √[(15 - 14)² + (17 - 17)²]

= √(1)² 

r = 1

r = 1 substitute the equation (1).

 (x - 14)² + (y - 17)²  = 1²

 (x - 14)² + (y - 17)²  = 1

Problem 9 :

Center : (-11, -8), Radius : 4

Solution :

Center of the circle is (x - h)² + (y - k)² = r²

Where h = -11 and k = -8

 (x + 11)² + (y + 8)² = 4² 

 (x + 11)² + (y + 8)² = 16

Problem 10 :

Center : (-6, -15), Radius : √5

Solution :

Center of the circle is (x - h)² + (y - k)² = r²

h, k is  -6, -15

 (x + 6)² + (y + 15)² = (√5)² 

 (x + 6)² + (y + 15)² = 5

Problem 11 :

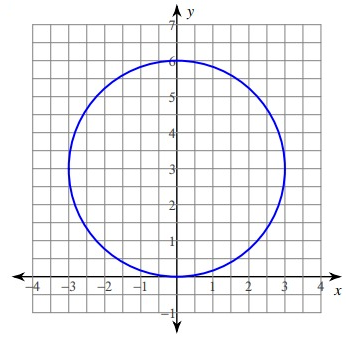
Solution :

By observing the figure,

Center : (0, 3)

Radius : 3

Center of the circle is (x - h)² + (y - k)² = r²

Where h = 0 and k = 3

 (x - 0)² + (y - 3)² = 3² 

 x² + (y - 3)² = 9

Problem 12 :

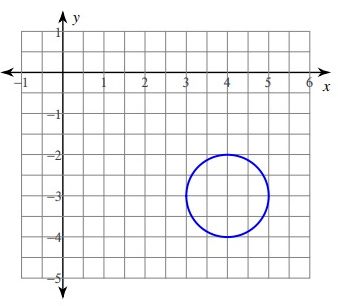
Solution :

By observing the figure,

Center : (4, -3)

Radius : 1

Center of the circle is (x - h)² + (y - k)² = r²

Where h = 4 and k = -3

 (x - 4)² + (y + 3)² = 1² 

 (x - 4)² + (y + 3)² = 1