FIND DOMAIN RANGE X AND Y INTERCEPT IN LOGARITHMS

The logarithmic function is the inverse of exponential function.

f(x) = log_a(ax + b) + c

Finding domain :

Domain is set of all possible defined values of x. To find domain of logarithmic function, we can use the procedure given below.

Step 1 :

Take the argument and create the condition,

(ax + b) > 0

Step 2 :

Get the possible values of x from the above condition.

For example,

f(x) = log4 x x > 0
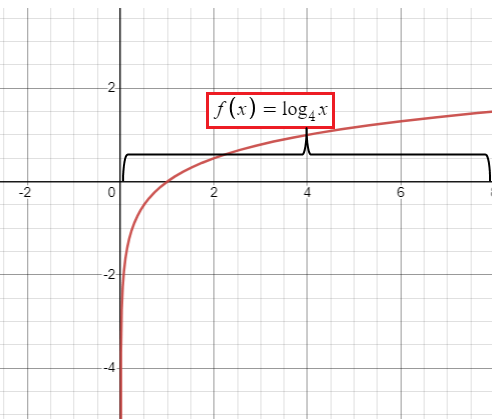f(x) = log4(x-2) x - 2 > 0 x > 2

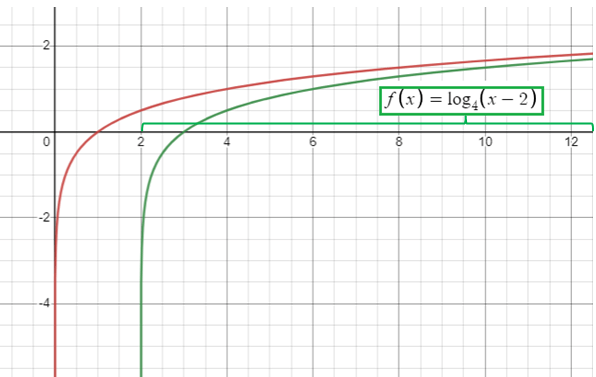Range :

Set of possible values of y is range. 

x-intercept :

The curve where it is intersecting the x-axis is known as x-intercept. To find x-intercept, we have to set up y to 0.

y-intercept :

The curve where it is intersecting the y-axis is known as y-intercept. To find y-intercept, we have to set up x to 0.

For the following exercises, state the domain, range, and x- and y-intercepts, if they exist. If they do not exist, write DNE.

Problem 1 :

h(x) = log₄(x - 1) + 1

Solution:

Considering the parent function as f(x) = log₄x

the given function h(x) = log₄(x - 1) + 1

should be translated 1 unit to the right and 1 unit up.

Finding domain :

To find domain, we have to set up the condition argument > 0

x - 1 > 0

x > 1

Finding range :

All real numbers.

x-intercept:

h(x) = 0

0 = log₄(x - 1) + 1

log₄(x - 1) = -1

x - 1 = 4^-1

x - 1 = 1/4

x = 1/4 + 1

x = 5/4

x- intercept = (5/4, 0)

y- intercept:

x = 0

h(x) = log₄(0 - 1) + 1

h(x) = log₄(-1) + 1

Does not exist

Problem 2 :

f(x) = log(5x + 10) + 3

Solution:

Domain:

5x + 10 > 0

5x > -10

x > -2

Domain: {x € R |x > -2}

Range:

The range of the function is set of real numbers.

x- intercept:

y = 0

0 = log(5x + 10) + 3

log(5x + 10) = -3

5x + 10 = 10^-3

5x + 10 = 1/10³

5x + 10 = 1/1000

5x = (1/1000) - 10

5x = -9999/1000

x = -9999/5000

y- intercept:

x = 0

y = log(5x + 10) + 3

y = log(5(0) + 10) + 3

y = 4

Problem 3 :

g(x) = ln(-x) - 2

Solution:

g(x) = ln(-x) - 2

Domain:

-x > 0

x < 0

Domain: (-∞, 0)

Range:

All real numbers

x- intercept:

y = 0

ln(-x) - 2 = 0

ln(-x) = 2

-x = e²

x = -e²

y- intercept:

x = 0

g(x) = ln(0) - 2

Does not exist.

Problem 4 :

f(x) = log₂(x + 2) - 5

Solution:

f(x) = log₂(x + 2) - 5

Domain:

x + 2 > 0

x > -2

Domain: (-2, ∞)

Range:

All real numbers

x- intercept:

y = 0

log₂(x + 2) - 5 = 0

log₂(x + 2) = 5

x + 2 = 2⁵

x + 2 = 32

x = 32 - 2

x = 30

y- intercept:

x = 0

f(0) = log₂(0 + 2) - 5

= log₂(2) - 5

= 1 - 5

f(0) = -4

Problem 5 :

h(x) = 3ln(x) - 9

Solution:

h(x) = 3ln(x) - 9

Domain:

x > 0

Domain: (0, ∞)

Range:

All real numbers

x- intercept:

y = 0

3ln(x) - 9 = 0

ln(x) = 9/3

ln(x) = 3

x = e³

y- intercept:

x = 0

h(0) = 3ln(0) - 9 

Does not exist.