FIND DOMAIN OF RATIONAL FUNCTION WITH RADICAL AS INTERVAL NOTATION

State the domain in interval notation.

Problem 1 :

Solution:

Equate the denominator to zero.

x - 3 = 0

x = 3 

If x = 3, then the denominator becomes zero and the value of 'y' becomes undefined.

So, 'y' is defined for all real values of 'x' except x = 3.

Therefore, the domain is

R - {3}

In interval notation,

(-∞, 3)∪(3, ∞)

Problem 2 :

Solution:

Equate the denominator to zero.

x² - 25

x² - 5² = 0

Using algebraic identity a² - b² = (a + b)(a - b)

(x + 5)(x - 5) = 0

x + 5 = 0 or x - 5 = 0

x = -5 or x = 5

The domain is all real values except -5 and 5.

In interval notation,

(-∞, -5)∪(-5, 5)∪(5, +∞)

Problem 3 :

Solution:

Equate the denominator to zero.

x² + 4x - 21 = 0

x² + 7x - 3x - 21 = 0

x(x + 7) - 3(x + 7) = 0

(x + 7) (x - 3) = 0

x = -7 or x = 3

The domain is all real values except -7 and 3.

In interval notation,

(-∞, -7)∪(-7, 3)∪(3, +∞)

Problem 4 :

Solution:

Equate the denominator to zero.

3x² + 9x = 0

3x(x + 3) = 0

3x = 0 or x + 3 = 0

x = 0 or x = -3

The domain is all real values except 0 and -3.

In interval notation,

(-∞, -3)∪(-3, 0)∪(0, +∞)

Problem 5 :

Solution:

2x - 8 = 0

x = 4

√(x²- 36) ≥ 0

x²- 36 ≥ 0

x² ≥ 36

x ≥ ±6

Decomposing into intervals.

(-∞, -6), (-6, 4) (4, 6) and (6, ∞)

Domain is (-∞, -6) U (6, ∞).

Problem 6 :

Solution:

3x - 24 = 0

x = 8

√(x²- 25) ≥ 0

x²- 25 ≥ 0

x² ≥ 25

x ≥ ±5

Decomposing into intervals.

(-∞, -5), (-5, 5) (5, 8) and (8, ∞)

So, the domain is (-∞, -5),(5, 8) and (8, ∞).

Problem 7 :

Solution:

x²+7x+10 = 0

(x + 5)(x + 2) = 0

x = -5 and x = -2

√(9 - x²) ≥ 0

9 - x² ≥ 0

-x² ≥ -9

x² ≤ 9

x ≥ ±3

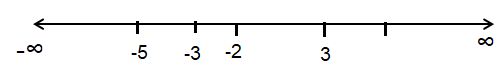
Decomposing into intervals.

(-∞, -5), (-5, -3) (-3, -2), (-2, 3) and (3, ∞)

So, the domain is (-3, -2) and (-2, 3).

Problem 8 :

Solution :

√(5x³ - 9) ≥ 0

For all negative values of x, we will get negative values. So, only positive values are applicable.

(5x³ - 9) = 0

5x³ = 9

x³ = 9/5

x = cube root (1.8) ==> 1.216

Equating the denominator to 0, we get

x³ +13x² + 42x = 0

x(x² +13x + 42) = 0

x(x + 6)(x + 7) = 0

x = 0, x = -6 and x = -7

Here all these values should be excluded from domain. So, the required domain is x ≥ 1.216