FIND DOMAIN AND RANGE OF ABSOLUTE VALUE FUNCTION FROM GRAPH

What is domain from graph ?

The horizontal spread or the spreading over the x-axis is knowns as domain.

The vertical spread or the spreading over the y-axis is knowns as range.

For absolute value function, which is in the form of 

y = a |x-h| + k

the domain will be all real values.

For example, considering the graph given below.

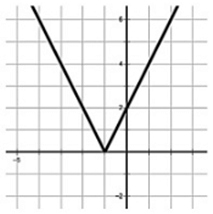
Domain :

The horizontal spread of the graph, or the spreading over all the x-axis. So, domain is {-∞, ∞}.

Range :

The vertical spread of the graph, or the spreading is above 0 on y-axis. So, range is {0, ∞}.

From each graph :

(i)  Find vertex and write a function

(ii) State the domain and range

(iii) Intercept

(iv) axis of symmetry

Problem 1 :

Solution :

Equation of the function :

General form of absolute value function is y = a|x - h| + k

Vertex is at (-1, 0), the absolute value function is passing through the point (0, 2).

Applying the vertex,

y = a|x - (-1)| + 0

y = a|x + 1|

Applying the point (0, 2), we get

2 = a |0 + 1|

2 = a

So, the required function is

f(x) = 2|x + 1|

Domain :

All real value is domain.

Range :

[0, ∞), y ≥ 0

Axis of symmetry :

x = -1

Maximum / Minimum :

Minimum

Problem 2 :

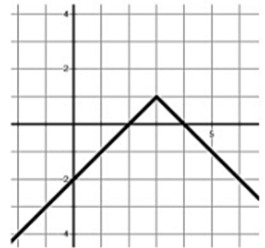
Solution :

Equation of the function :

General form of absolute value function is y = a|x - h| + k

Vertex is at (3, 1), the absolute value function is passing through the point (4,0).

Applying the vertex,

y = a|x - 3| + 1

Applying the point (4, 0), we get

0 = a |4 - 3| + 1

-1 = a

a = -1

So, the required function is

f(x) = -|x - 3| + 1

Domain:

All real value is domain.

Range:

[1,-∞), y ≤ 1

Axis of symmetry:

x = 3

Maximum / Minimum

Maximum