FIND DERIVATIVE OF Y WITH RESPECT TO X WITH SUBSITUTIONS OF U AND V

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

In differential calculus, the chain rule is a formula used to find the derivative of a composite function.

If y = f(g(x)), then as per chain rule the instantaneous rate of change of function 'f' relative to 'g' and 'g' relative to x results in an instantaneous rate of change of 'f' with respect to 'x'.

chain-rule-defintion

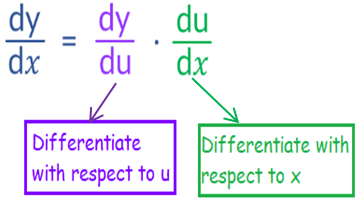
Problem 1 :

y=2u2, u=3v, v = 2x+1 at x = 0

Solution :

y=2u2, u=3v, v = 2x+1dydu=2(2u) ≡> 4u ----(1)dudv=3(1) ≡> 3 ----(2)dvdx=2(1)+0 ≡> 2 ----(3)(1)×(2)×(3)dydx=dydu×dudv×dvdx= 4u×3×2= 24uApplying the value of u, we getdydx= 24(3v)Applying the value of v, we getdydx= 72(2x+1)Applying the value of x=0dydx= 72(2(0)+1)= 72

Problem 2 :

y=5+2u, u=2v-3, v =1-4x at x =

Solution :

y=5+2u, u=2v-3, v =1-4x at x = 1dydu=0+2(1) ≡> 2 ----(1)dudv=2(1)-0 ≡> 2 ----(2)dvdx=0-4(1)≡>-4 ----(3)(1)×(2)×(3)dydx=dydu×dudv×dvdx= 2×2×(-4)= -16

Problem 3 :

y=4u3-3u2, u=2v2+4v, v=1-2x2 at x=

Solution :

y=4u3-3u2, u=2v2+4v, v=1-2x2 at x=dydu=43u2-3(2u)≡>12u2-6u ----(1)dudv=2(2v)+4(1)≡> 4v+4 ----(2)dvdx=0-2(2x)≡>-4x ----(3)(1)×(2)×(3)dydx=dydu×dudv×dvdx= 12u2-6u×(4v+4×Applying the value of u, we getdydx= 122v2+4v2-62v2+4v×41-2x2+4×Applying the value of v, we getdydx= 1221-2x22+41-2x22-621-2x22+41-2x2×41-2x2+4××(4(-1)+4×

Problem 4 :

y=2+u, u=2+v, v=2+x at x=

Solution :

y=2+u, u=2+v, v=2+x at x=dydu=122+u ----(1)dudv=122+v ----(2)dvdx=122+x ----(3)(1)×(2)×(3)dydx=dydu×dudv×dvdx=122+u×122+v ×122+xdydx= 18(2+u)(2+v)(2+x)= 18(2+u)(2+v)(2+2)= 116(2+u)(2+v)= 1164+22+2+x+2+x+2+2+x2+x= 1164+22+2+2+2+2+2+2+22+2= 116(4+2(2+2)+2(2))= 11616= 164

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More