FIND COMPOSITION OF TWO FUNCTIONS FROM TABLE

To find composition of two functions from the table, we have to follow the procedure given below.

Example :

From the table given below,

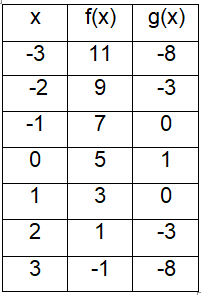
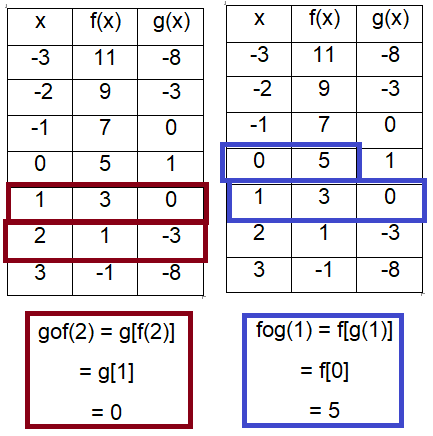
find i)  [gof] (2)     ii)  [fog] (1)

Problem 1 :

The domain of function f is

{-3, -1, 0, 1, 3}

and the domain of g is 

{-1, 0, 1, 3, 5}

The rule for f and g are the tabular form.

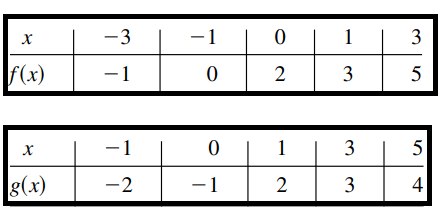
(a) Complete the following table for g ∘ f. If an entry is undefined write U. 

b) What is the domain of g ∘ f ?

c) What is the domain of f ∘ g ?

Solution :

a) To complete the table,

[g ∘ f ](x) = g[f(x)]

When x = -3

[g ∘ f ](-3) = g [f(-3)]

By observing the table f, the output for -3 is -1. So, f(-3) = -1

= g [-1]

By observing the table g, the output for -1 is -2. So, g(-1) = -2

= -2

Then,

[g ∘ f ](-3) = -2

b)  Domain of g ∘ f is 

{ -3, -1, 1, 3}

Reason of excluding 0 :

Because for the input 0, we get undefined value. So, we exclude 0 from domain.

c)  To find Domain of f ∘ g, first let us find the composition.

[f ∘ g ](x) = f[g(x)]

When x = -1

[f ∘ g ](-1) = f [g(-1)]

By observing the table g, the output for -1 is -2. So, f(-1) = -2

= f [-2]

By observing the table f, we don't see the input -2 for f(x). So, it is undefined.

Then,

[f ∘ g ](-1) = U

So, the domain of [f ∘ g ](x) is,

= {0, 3}

Problem 2 :

Graphs of the functions f and g are shown. Complete the following tables.

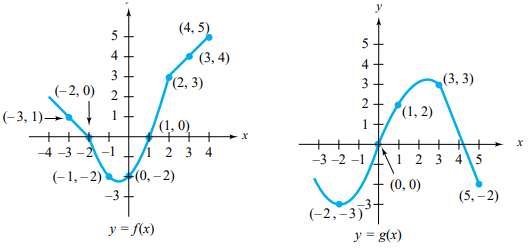
Solution :

Points from the graph f(x) :

(-3, 1) (-2, 0) (-1, -2) (0, -2) (1, 0) (2, 3) (3, 4) and (4, 5)

Points from the graph g(x) :

(-2, -3) (0, 0) (1, 2) (3, 3) and (5, -2)

[g ∘ f ](x) = g[f(x)]

We give inputs from f, from the table

When x = -3, x = 0, x = 1, x = 2 and x = 4

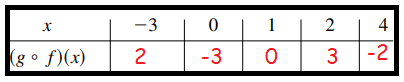
i) For x = -3

From the points from the graphs f and g,

(-3, 1) ==> (1, 2) ==> 2

ii) For x = 0

From the points from the graphs f and g,

(0, -2) ==> (-2, -3) ==> -3

iii) For x = 1

From the points from the graphs f and g,

(1, 0) ==> (0, 0) ==> 0

iv) For x = 2

From the points from the graphs f and g,

(2, 3) ==> (3, 3) ==> 3

v) For x = 4

From the points from the graphs f and g,

(4, 5) ==> (5, -2) ==> -2

[f ∘ g ](x) = f[g(x)]

We give inputs from g, from the table

When x = -2, x = 0, x = 1, x = 3 and x = 5

i) For x = -2

From the points from the graphs g and f,

(-2, -3) ==> (-3, 1) ==> 1

ii) For x = 0

From the points from the graphs g and f,

(0, 0) ==> (0, -2) ==> -2

iii) For x = 1

From the points from the graphs g and f,

(1, 2) ==> (2, 3) ==> 3

iv) For x = 3

From the points from the graphs g and f,

(3, 3) ==> (3, 4) ==> 4

v) For x = 5

From the points from the graphs g and f,

(5, -2) ==>(-2, 0) ==> 0