FIND AREA WHOLE AND HALF UNITS OF LENGTH

Find the area of the following figures.

Each square stand for 1 square unit and each triangle stands for a half square unit.

Problem 1 :

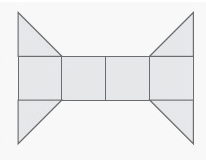
Solution :

Total number of square = 4

Area of complete squares

= number of squares x area of each square

= 4 × 1

Area of squares = 4

Total number of triangles = 4

Area of triangles = 4 × 0.5

= 2

Required area = 4 + 2

= 6 square units

Problem 2 :

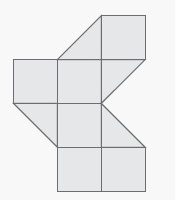
Solution :

By observing the figure,

Total number of square = 6

= 6 × 1

= 6

Total number of triangle = 4

= 4 × 0.5

= 2

Required area = 6 + 2

= 8 square units

Problem 3 :

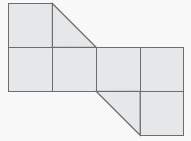
Solution :

Total number of square = 6

Area of squares = 6 × 1  ==> 6

Total number of triangle = 2

Area of triangles = 2 × 0.5  ==> 1

Area of the shaded portion = 6 + 1

= 7 square units

Problem 4 :

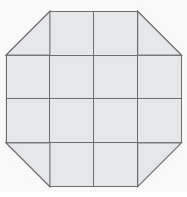
Solution :

Total number of square = 12

Area of shaded squares = 12 × 1 ==> 12

Total number of triangle = 4

Area of shaded triangles = 4 × 0.5 ==> = 2

Total number of area = 12 + 2

= 14 square units

Problem 5 :

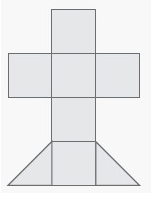
Solution :

Total number of square = 6

Area of squares = 6 × 1 ==> 6

Total number of triangle = 2

Area of triangles = 2 × 0.5 ==> 1

Area of shaded portion = 6 + 1

= 7 square units

Problem 6 :

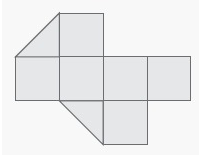
Solution :

Total number of square = 6

Area of shaded squares = 6 × 1 ==> 6

Total number of triangle = 2

Area of shaded triangles = 2 × 0.5 ==> 1

Required area = 6 + 1

= 7 square units

Problem 7 :

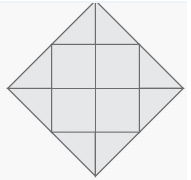
Solution :

Total number of square = 4

Area of shaded squares = 4 × 1 ==> 4

Total number of triangle = 8

Area of shaded triangles = 8 × 0.5 ==> 4

Required area = 4 + 4

= 8 square units

Problem 8 :

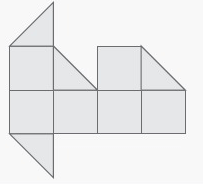
Solution :

Total number of square = 6

Area of shaded squares = 6 × 1 ==> 6

Total number of triangle = 4

Area of shaded triangles = 4 × 0.5 ==> 2

Required area = 6 + 2

= 8 square units

Problem 9 :

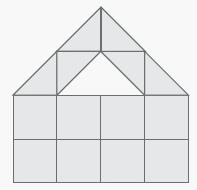
Solution :

By observing the figure,

Total number of square = 8

Area of shaded squares = 8 × 1 ==> 8

Total number of triangle = 6

Area of shaded triangles = 6 × 0.5 ==> 3

Required area = 8 + 3

= 11 sq.units