FIND AREA OF SQUARE WHEN DIAGONAL IS GIVEN

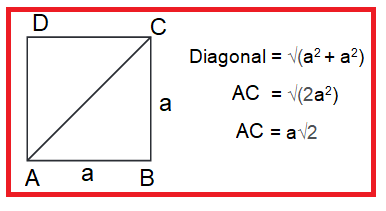
Let us consider the following square.

Problem 1 :

Find the area of a square with a diagonal of 3 cm.

Solution :

Diagonal = 3 cm

Diagonal d = √2 a

√2 a = 3

a = 3/√2

a = 3/1.414

a = 2.121

Area of square = a²

= (2.121)²

= 4.5 cm²

So, area of a square is 4.5 cm².

Problem 2:

Find the area of a square whose diagonal is 9 cm.

a) 18 cm²   b) 81/2 cm²     c) 36 cm²    d) 81 cm²

Solution :

Given, diagonal = 9 cm

Diagonal d = √2 a

√2 a = 9

a = 9/√2

Area of square = a²

= (9/√2)²

= 81/2 cm²

So, option (b) is correct.

Problem 3:

The area of a square is 2√2 + 3. What is the length of a side of the square?

a) √2 - 1    b) 2√2 - 1    c) √2 + 1    d) 2√2 + 1

Solution :

Area of square =  2√2 + 3

a² =  2√2 + 3

So, side length of the square is √2 + 1.

Problem 4 :

The area of the square ABCD is 9/2 cm². Find the length of BD.

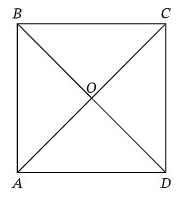
Solution :

Given, area of a square = 9/2 cm²

Area = a²

9/2 = a²

a = √ (9/2)

a = 3/√2 cm

a = 3/1.414

a = 2.12 cm

So, length of a square is 2.12 cm.

Problem 5 :

Find the area of a square one of whose diagonal is 3.8 m long.

Solution :

Diagonal d = √2 a

√2 a = 3.8

a = 3.8/√2

a = 3.8/1.414

a = 2.687

Area of square = a²

= (2.687)²

= 7.22 m²

So, area of a square is 7.22 m².

Problem 6:

The diagonals of two squares are in the ratio 2 : 5. Find the ratio of their areas.

Solution :

Let the diagonals of first and second square be 2x and 5x respectively.

Ratio of area = 2x²: 25x²/2

= 2 : 25/2

= 4 : 25

Therefore the ratio of the areas of two squares is 4 : 25.

Problem 7 :

A man walked diagonally across a square lot. Approximately, what was the percent saved by not walking along the edges?

a) 20       b) 24       c) 30       d) 33

Solution :

Diagonal of square = √2 a

= 1.414 a

When you walk on two sides of square = 2a

When you walk diagonally = 1.414 a

Percentage saving = [(2a - 1.414a)/2a] × 100

= 29.5%

Therefore, percentage saving is 29.5% (approx)

So, option (c) is correct.

Problem 8 :

A man walking at the speed of 4 kmph crosses square field diagonally in 3 minutes. The area of the field is.

a) 18000 m²    b) 19000 m²  c) 20000 m²   d) 25000 m²

Solution :

Speed of man = 4 km/hr

= 4000/60 m per min

Distance covered in 3 minutes = 3 × 4000/60

= 200 meter

Diagonal of square = 200 meter

Area of square = 1/2 × (diagonal)²

= 1/2 × 200 × 200

= 20000 square meter

So, option (c) is correct.

Problem 9 :

If the length of the diagonal of a square is 20 cm, then its perimeter must be

a) 10√2 cm      b) 40 cm    c) 40√2 cm     d) 200 cm

Solution :

Diagonal of a square = √2 a

Side = diagonal/√2

= 20/√2 cm

= 20/√2 × √2/√2

= 10√2 cm

Perimeter of square = 4 a

= 4 × 10√2

= 40√2 cm

So, option (c) is correct.

Problem 10 :

The area of a square field is 69696 cm². its diagonal will equal to.

a) 313.296 m      b) 353.596 m

c) 373.296 m      d) 393.296 m

Solution :

The area of a square = 69696 cm²

Area = a²

a = √69696

a = 264 cm

Diagonal = √2 a

= √2 × 264

= 1.414 × 264

= 373.296 m

So, option (c) is correct.