FIND AMPLITUDE PERIOD PHASE SHIFT AND VERTICAL SHIFT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The graph of y = A sin (Bx - C) + D is obtained by horizontally shifting the graph of y = A sin Bx so that the starting point of the cycle is shifted from x = 0 to x = C/B.
- If C/B > 0, the shift to the right
- If C/B < 0, the shift to the left.
- If C/B is 0, then there is no phase shift.
The number C/B is called Phase shift.
Amplitude = |A|
Period = 2
- If D > 0, shift up
- If D < 0, shift down.
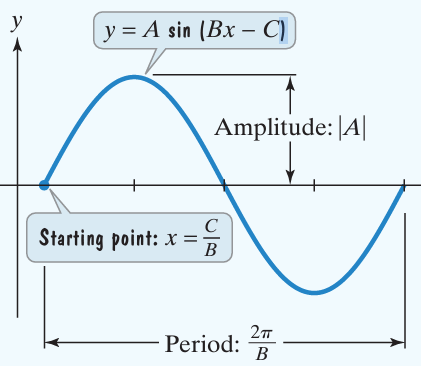
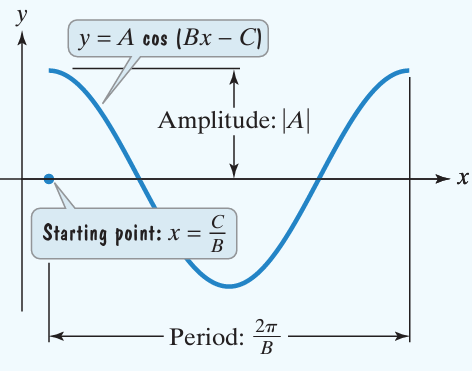
Determine the amplitude, period, phase shift and vertical shift for each.
Problem 1 :
Solution :
Comparing the given function with y = A sin (Bx - C) + D
A = 3, B = 4, C = -𝜋/2 and D = 2
Finding amplitude :
Amplitude = 3
Finding period :
Period = 2𝜋/|B|
= 2𝜋/4
= 𝜋/2
Finding Phase shift :
C/B = (-𝜋/2)/4
= -𝜋/8 < 0
Moving the graph towards left of 𝜋/8.
Finding vertical shift :
D = 2 > 0
Moving the graph 2 units up.
Problem 2 :
Solution :
Comparing the given function with y = A cos (Bx - C) + D
A = 2, B = 1, C = 0 and D = -4
Finding amplitude :
Amplitude = 1/2
Finding period :
Period = 2𝜋/|B|
= 2𝜋/2
= 𝜋
Finding Phase shift :
C/B = 0/2
= 0
Then there is no phase shift.
Finding vertical shift :
D = -4 < 0
Moving the graph 4 units down
Problem 3 :
Solution :
Comparing the given function with y = A cos (Bx - C) + D
A = 2, B = 1, C = 𝜋 and D = 0
Finding amplitude :
Amplitude = 2
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding Phase shift :
C/B = 𝜋/1
= 𝜋 > 0
Horizontally move the graph right 𝜋.
Finding vertical shift :
D = 0
There is no vertical shift.
Problem 4 :
Solution :
Comparing the given function with y = A sin (Bx - C) + D
A = 4, B = 1, C = 𝜋 and D = -3
Finding amplitude :
Amplitude = 4
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding Phase shift :
C/B = 𝜋/1
= 𝜋 > 0
Horizontally move the graph right 𝜋.
Finding vertical shift :
D = -3
Move the graph down 3 units.
Determine the amplitude, period, phase shift and vertical shift of the function. Then graph one period of the function.
Problem 5 :
Solution :
Comparing the given function with y = A cos (Bx - C) + D
A = 1, B = 1, C = 𝜋/2 and D = 0
Finding amplitude :
Amplitude = 1
Finding period :
Period = 2𝜋/|B|
= 2𝜋/1
= 2𝜋
Finding Phase shift :
C/B = (𝜋/2)/1
= 𝜋/2 > 0
Horizontally move the graph right 𝜋/2.
Finding vertical shift :
D = 0
There is no vertical shift.
Finding x-coordinates of key points :
Starting point = Period / 4
= 2𝜋/4
= 𝜋/2
Using the phase shift, starting point is 𝜋/2.
|
Second point : = 𝜋/2 + 𝜋/2 = 2𝜋/2 = 𝜋 |
Third point : = 𝜋 + 𝜋/2 = (2𝜋 + 𝜋)/2 = 3𝜋/2 |
Fourth point : = 3𝜋/2 + 𝜋/2 = (3𝜋 + 𝜋)/2 = 4𝜋/2 = 2𝜋 |
Finding y-coordinates of key points :
|
|
|
|
|
|
So, the points are (𝜋/2, 1) (𝜋, 0) (3𝜋/2, -1) (2𝜋, 0). Plotting the points and joining the points, we will get the curve.
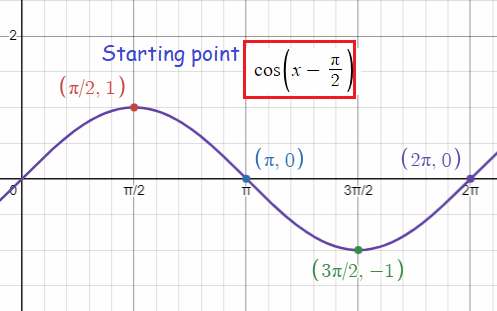
Problem 6 :
Solution :
Comparing the given function with y = A sin (Bx - C) + D
A = 4, B = 2, C = 2𝜋/3 and D = 0
Finding amplitude :
Amplitude = 4
Finding period :
Period = 2𝜋/|B|
= 2𝜋/2
= 𝜋
Finding Phase shift :
C/B = (2𝜋/3)/2
= 𝜋/3 > 0
Horizontally move the graph right 𝜋/3.
Finding vertical shift :
D = 0
There is no vertical shift.
Finding x-coordinates of key points :
Each point add upto = Period / 4
= 𝜋/4
First point is x = 𝜋/3
|
Second point : = 𝜋/3 + 𝜋/4 = 7𝜋/12 |
Third point : = 7𝜋/12 + 𝜋/4 = (7𝜋 + 3𝜋)/12 = 10𝜋/12 = 5𝜋/6 |
Fourth point : = 5𝜋/6 + 𝜋/4 = (10𝜋 + 3𝜋)/12 = 13𝜋/12 |
Fifth point :
= 13𝜋/12 + 𝜋/4
= (13𝜋 + 3𝜋)/12
= 16𝜋/12
= 4𝜋/3
Finding x-coordinates of key points :
x = 𝜋/3
|
|
|
|
|
|
So, the points are (𝜋/3, 0) (7𝜋/12, 4) (5𝜋/6, 0) (13𝜋/12, -4) (4𝜋/3, 0). Plotting the points and joining the points, we will get the curve.
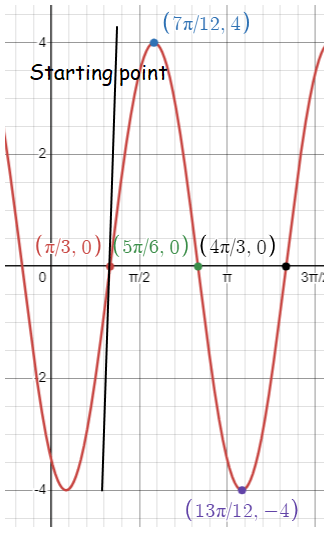
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling